「物理って難しい…」と感じているキミ。今回は、「力のつり合い」について、図解と練習問題を交えながら、とことん丁寧に解説していきます。学んだあとは、練習問題に挑戦して、理解を深めよう！
1. 「力のつり合い」ってどんな状態？：綱引き対決でイメージしよう！
「つり合い」と言われて、何を思い浮かべるかな？ 例えば、運動会の綱引きを想像してみよう！
両チームが同じ力で引っ張り合っていたら、綱は動かず、ピタッと止まった状態になるよね。これがまさに、「力のつり合い」の状態なんだ！
2. 力のつり合いの条件：3つのポイントをクリアせよ！
では、どんな条件が揃えば、力はつり合うのだろうか？ それは、次の3つのポイントだ！
ポイント①：ターゲットは一つ！：同じ綱を引っ張ろう！
力を加える相手は、同じ物体じゃなきゃダメだ！ 綱引きで、君たちのチームは綱を引っ張っているのに、相手チームが全く別の綱を引っ張っていたら勝負にならないよね？
ポイント②：一直線上で反対向き！：綱を引っ張り合おう！
力は、同じ直線上でお互いに反対向きに働いていないとダメだ！ 君たちのチームが右に、相手チームが左に引っ張れば、綱はピーンと張るけど、同じ方向に引っ張ったら、ズルズル引っ張られてしまうよね？
ポイント③：力の強さはピッタリ同じ！：力の限り引っ張り合おう！
力は、同じ強さじゃないとダメだ！ 君たちのチームが相手チームより弱かったら、綱は相手チーム側に引っ張られてしまうよね？
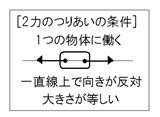
この3つのポイントが揃うと、物体は動かず、綱引きで綱がピタッと止まった状態、つまり「つり合った」状態になるんだ！
3. 身近な力：垂直抗力と摩擦力を解明せよ！
世の中には、目には見えないけど、いろいろな力が働いているぞ！ その中でも、特に重要なのが「垂直抗力」と「摩擦力」だ！
3-1. 垂直抗力：支える力！：君を支える床の力！
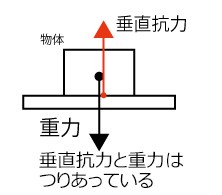
例えば、君が床の上に立っているとき、地球から「重力」を受けているよね？ でも、君は床を突き破って落ちていかない。それは、床が君を支える力、つまり「垂直抗力」が上向きにはたらいているからなんだ！
この垂直抗力は、接触している面に対して垂直な向きにはたらく力なんだ。
このとき、君にはたらく重力と、床から君にはたらく垂直抗力は、力のつり合いの関係になっている。だから、君は地面にめり込んだり、空中に浮いたりせずに、じっと立っていられるんだ。
3-2. 摩擦力：動きを邪魔する力！：もうちょっとで動かせそう！
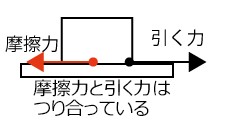
重いダンボール箱を押して、動かそうとした経験はないかな？ 最初は、なかなか動かないけど、力を入れ続けると、ようやく動き出すよね！
これは、床とダンボール箱の間に、「摩擦力」という力が働いて、動きを邪魔しているからなんだ。摩擦力は、物体が動こうとする向きと反対方向に働く力なんだ。
ダンボール箱が静止している間は、人が箱を押す力と、床から箱に働く摩擦力は、力のつり合いの関係になっているんだ。だから、箱は動き出さずにその場にとどまっているんだね。
[例題1]
静止しているダンボール箱を100 Nの力で押したら、動き出した。このダンボール箱にはたらいていた静止摩擦力の大きさは？
[解答1]
ダンボール箱が動き出すまでは、静止摩擦力と押す力はつり合っている。
よって、静止摩擦力の大きさは、押す力と同じ100 Nである。
4. 力の合成と分解：複数の力をまとめたり、分けたりするワザ！
複数の力が同時に働いている場合は、「力の合成」と「力の分解」を使えば、力をもっと簡単に考えることができるんだ！
4-1. 力の合成：2つの力を1つにまとめる！
例えば、君と友達が、それぞれ違う方向にロープを引っ張っているとしよう。この2つの力を合わせた結果、ロープはどう動くかな？ これを考えるのが「力の合成」だ！
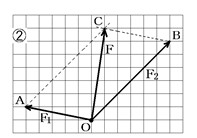
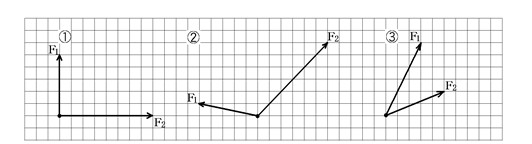
- 2つの力を矢印で書く:
合成したい2つの力を、矢印を使って表す。図のF1とF2。矢印の長さは力の大きさを、矢印の向きは力の向きを表す。 - 平行四辺形を描く:
F1の先端を通りF2に平行な線を引く。F2の先端を通りF1に平行な線を引く。F1とF2を隣り合う2辺とする平行四辺形ができた。 - 対角線が合力:
できた平行四辺形の対角線が、F1とF2を合成された力、つまり「合力」を表す。
4-2. 力の分解：1つの力を2つに分ける！
反対に、1つの力を、2つ以上の力の組み合わせで表すこともできる。これが「力の分解」だ！
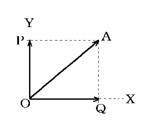
- 分解したい力と2つの向きを決める:
分解したい力OAを矢印で書き、分解する方向をきめる（図ではOXとOY方向に分解する）。 - 平行四辺形を描く:
OAの先端を通り、OXに平行な線を引きOYとの交点をPとする。同様に、OAの先端を通り、OYに平行な線を引きOXとの交点をQとする。OAを平行四辺形の対角線とする平行四辺形（OQAP）ができている。 - 2辺が分力:
できた平行四辺形の2辺（OQとOP）が、OAが分解された力、つまり「分力」を表す。
5-1. 練習問題に挑戦！
練習1
次の①～③で、F1とF2の合力を作りなさい。
解答1
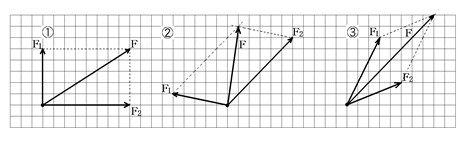
練習2
次の①～③で、矢印の力を点線方向の2力に分解しなさい。
解答2
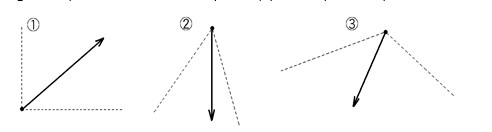
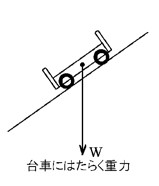
練習3
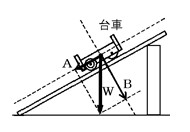
図を見てください。矢印Wは物体にはたらいている重力を示しています。
(1) 重力Wを、斜面に沿った方向の力Aと、斜面に垂直な方向の力Bの2つに分けてみよう。
(2) こうやって分けた2つの力のことを何て言うかな？
(3) 斜面が急になると、力Aはどうなりますか？
(4) （1）のBに釣り合う力は何かな？
解答3
（1）
（2） 分力 （3）大きくなる （4）垂直抗力
【作図のしかた】 重力は、斜面上では必ず、斜面に平行な方向と斜面に垂直な方向に分解されます。
Wの先端から斜面に平行な方向と斜面に垂直な方向に平行線を引きます。
斜面に垂直な直線と交わった点をＢ： 台車が、斜面を垂直に押す力
斜面に平行な直線を交わった点をA： 台車が、斜面に沿って落ちる力
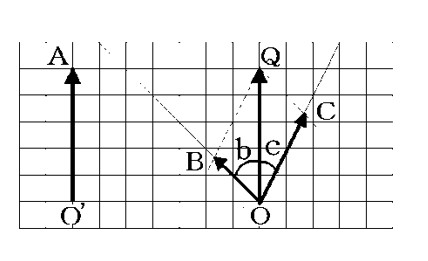
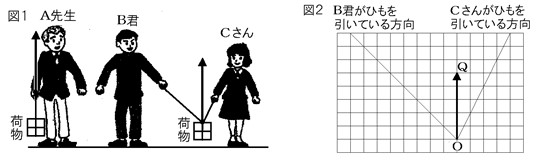
練習4
図1を見てね。6kgの物Aを先生が1人で持ってるのに対して、B君とCさんは2人でひもを引っ張って支えてるよ。
先生が引っ張ってる力をPとし、B君とCさんが2人で引っ張ってる力の合計をQとするね。ここで、100gの物体にはたらく重力は1Nと考えるよ。ひもの重さは無視していいよ。
(1) 先生の引っ張ってる力Pは、何Nかな？
(2) B君が引っ張ってる力と、Cさんが引っ張ってる力を図2の点Oから矢印で表してみよう。
(3) 3人がそれぞれひもを引っ張っている力の強さを、大きい順にA～Cで並べてみてね。
練習4
（1）60N （2） 下図 （3） A、C、B
（2）【作図の方法】Qを通り，B君のひもの方向に平行な線とCさんのひもの方向に平行な線を引き，平行四辺形を描きます。Bさんの力がOB、Ｃさんの力がOC
（3）OA、OB、OCの長さを比べると、A、C、Bの順に長いので、力の大きさは、A、C、Bの順です。
5. まとめ：力のつり合いで物理を攻略せよ！
今回は「力のつり合い」について、図解と練習問題を交えながら解説したぞ！ 学んだことを活かして、物理の問題に挑戦してみよう！ きっと、今までよりも解ける問題が増えているはずだ！ がんばれ！
😊「なんだ。簡単じゃん」と感じてもらえたらすごくうれしいです。わかりにくい問題があったら、教えてください。簡単に説明したり、わかりやすい他の方法で、もっと楽に理解が深まります。
「ブログより実際に話しがしたい」「もっといろいろ教えてほしい！」と感じた人は、無料体験や相談に来てください！ この先生に相談をすることや習うことができます！ 少し勇気を出して、ぜひ一度体験しに来てください！ 「わかるって面白い」とか成績が良くなる自分を感じられる日がきます。お問い合わせ・ご質問はこちらです。
