🎬 ゆうと&あかりのストーリー解説
二次関数 × 図形の問題をスッキリ攻略!
🧩 問題
放物線①: \( y = \frac{1}{3}x^2 \)放物線②:\( y = ax^2 \)
x軸に平行な直線③があり、これが2つの放物線と点A, B, C, Dで交わっている。
線分AC、CD、DBの長さは等しい(AC=CD=DB)。
点Bのx座標は6である。
このとき、aの値を求めよ。
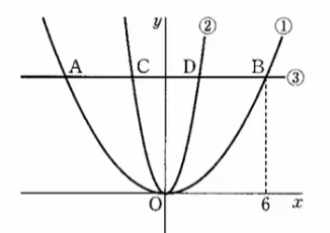
👦 ゆうと:「うわっ、放物線が2つも出てきた!しかも“線分が全部同じ長さ”とか書いてあるし…。どこから手をつければいいんだろう?」
👧 あかり:「見た目にびっくりするけど、こういうときのコツはね――
“まず、1点ずつ座標を求めて整理!” なんだよ。文字が入ってても大丈夫。
“わかる点から順に”出していこう!」
🪄 ステップ1:点Bの座標を求めよう
👧 あかり:「Bは放物線①: \( y = \frac{1}{3}x^2 \)の上にあって、x=6だね式に代入してみよう。」
👦 ゆうと:「 \( y = \frac{1}{3}×(6)^2 \)=12! だから B(6,12)」
👧 あかり:「OK! 同じ高さにあるAは、Bとy軸対称だから、xだけ反対にすればいいよ。A(−6,12)」
👦 ゆうと:「あっ、放物線って左右対称だから簡単に出せるんだ!」
🪄 ステップ2:線分を3等分して考えよう
👧 あかり:「AとBのx座標の差は 6 − (−6)=12。
これを3等分するんだから、1区間の長さは4だね。」
👦 ゆうと:「なるほど!つまりA→Bの間を3つに分ける感じか。
じゃあ、A(−6,12)から順に4ずつ増えていくから、C(−2,12)、D(2,12)、B(6,12)…って感じだ!」
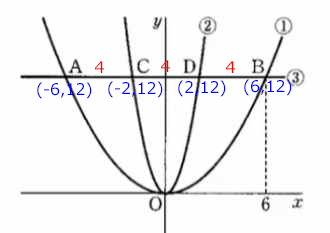
👧 あかり:「いいね!イメージでは、放物線の上で小さな“橋”を3本並べたような感じだね。」
🪄 ステップ3:aの値を求めよう
👦 ゆうと:「D(2,12)はもう一つの放物線 y=ax² の上にあるから、代入しよう!」
👧 あかり:「うん、a×2²=12 だから、 a=3 だね!」👦 ゆうと:「わかった!2つ目の放物線は y=3x²。
最初に“座標を1個ずつ整理する”ってやり方、ほんとスッキリするね。」
👧 あかり:「でしょ?まず最初に各点の座標を求めるを進めていくと迷わないですむよ!」
🌱 もう1問挑戦!正方形が出てくる問題
放物線①: \( y = \frac{1}{4}x^2 \)放物線②:\( y = ax^2 \)
放物線上に4点A, B, C, Dがあり、四角形ABCDは正方形。
辺ABはx軸に平行で、Aのx座標は2である。
このとき、aの値を求めよ。
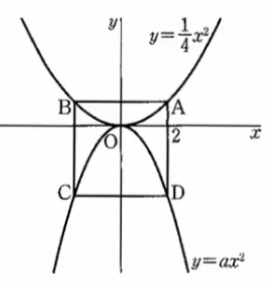
👦 ゆうと:「今度は“正方形”!? なんか急に難しそう!」
👧 あかり:「大丈夫。これもやることは一緒!まず、各点の座標を整理してみよう。」
A(2, 1)
B(−2, 1)
D(2, 4a)
C(−2, 4a)
👦 ゆうと:「すっごくシンプルになったね!」
👧 あかり:「でしょ? 図形の問題は“見える形”にすると一気に解けるんだよ。」
🪄 ステップ4:正方形の性質で式を立てよう
👧 あかり:「正方形だから、AB=AD。
横の長さABは、Aのx座標からBのx座標を引くから、 2 − (−2)=4。
縦の長さADは、Aのy座標からDのy座標を引くから、 1 − 4a だね。」
👦 ゆうと:「それで正方形だから、式は 1 − 4a=4 !」
👧 あかり:「そう!これを解くと a=−3/4!」
👦 ゆうと:「マイナスってことは、下に開く放物線なんだね!」
👧 あかり:「その通り! “正方形の縦と横が同じ”っていう形の性質を、数で表せばすぐ答えが出るの。
図形×関数の問題も、座標整理+性質の式化が最強だよ!」
🎯 放物線×図形の考え方Q&A(ゆうと&あかりの会話)
- Q1. 放物線と図形が出てきたとき、最初に何をすればいいの?
-
👦 ゆうと:「問題に放物線が2つとか、点A・B・C・Dが出てくると、どこから手をつけていいかわからなくなるんだけど…。」
👧 あかり:「まずやることはひとつ!“それぞれの点の座標を出すこと”。
グラフは難しく見えても、座標にすればただの数字の関係になるよ。
わかる点から順に、式に代入して座標を整理しよう!」👦 ゆうと:「なるほど、“見た目より先に数で整理”だね!」
💡ワンポイント:図形問題でも、最初の1歩は“座標で見える化”。
- Q2. 対称な点って、どうやってすぐに見つけられるの?
-
👦 ゆうと:「AとBが“y軸について対称”とかって書いてあるけど、
頭の中で反転させるのが難しいんだよね…。」👧 あかり:「コツは簡単!
y軸対称の点は “xの符号だけが反対” になるの。
たとえばB(6,12)なら、対称なAは(−6,12)。
これを“鏡にうつしたように反転”ってイメージすれば、すぐにわかるよ。」👦 ゆうと:「あ、なるほど!“xが反対、yは同じ”って覚えればいいんだ!」
💡ワンポイント:y軸対称 → xの符号だけ逆にする!
- Q3. 「長さが等しい」とか「正方形」とか出てきたときはどう考えればいいの?
-
👦 ゆうと:「“線分が等しい”とか“正方形”とか出ると、式にどうつなげていいかわからないんだよね。」
👧 あかり:「図形の“形の性質”を“数字の関係”に変えるのがコツ!
たとえば、線分が等しいなら“長さの式が同じ”ってこと。
正方形なら“縦と横の長さが同じ”。
つまり、“形の条件=式の条件”に置きかえるんだよ。」👦 ゆうと:「あ、図形の見た目を“数式で表す”ってことなんだね!」
💡ワンポイント:図形の性質は「長さ=長さ」「高さ=高さ」で式に変える!
- Q4. グラフって、やっぱり描いたほうがいいの?
-
👦 ゆうと:「正直、放物線のグラフを描くのってちょっと面倒なんだよね…。
描かずにできるようになりたいな。」👧 あかり:「気持ちはわかるけど、グラフは描いたほうが絶対いいよ。
ただね、ポイントは“やみくもに描かないこと”。
まず頭の中で『上に開くのか』『左右対称のどの辺に点があるのか』を考えてから描くと、
グラフが“考えるための道具”になるんだ。」👦 ゆうと:「あ、なるほど!描くのが目的じゃなくて、考えを整理するためなんだね。」
👧 あかり:「そうそう。だから、最初は必ず描いた方がいい。
でも、慣れてくると“頭の中で描ける”ようになってくるよ!」💡ワンポイント:グラフは“考えるために描く”。慣れたら、頭の中でもイメージできる!
- Q5. 文字が出てくるとき、どんなふうに考えればいいの?
-
👦 ゆうと:「a とか b とか、文字が出てくると急に難しく感じちゃうんだよね。」
👧 あかり:「実は、文字も“まだわからない数”ってだけ。
数字のかわりに文字を入れて式を作るだけで、やってることは全く同じなんだよ。
文字を使うと、いろんなパターンに使える“公式みたいな考え方”になるの。」👦 ゆうと:「そっか、“文字=変わる数”って思えば怖くないね!」
💡ワンポイント:文字は「動く数」。文字で整理すれば、どんな問題にも応用できる!
🌟 あかりからのまとめ
👧 あかり:「放物線と図形が出たら、焦らず“座標で整理”してみよう。
形の条件を“式で言いかえる”のが、最大のコツ!✨」
🧠 先生からの「ここだけは絶対に押さえろ!」
✅ ① 放物線×図形のときは、まず“座標を整理!”
放物線が2つ出てきたり、図形が組み合わさっていたりしても、
最初にやることは 「それぞれの点の座標を求める」 こと。
数字で整理すれば、見た目の複雑さに惑わされません。
📍ポイント:
わかっている点 → 式に代入 → 座標を整理
→ これで「どこにある点なのか」がハッキリ見える!
✅ ② 図形の“形の条件”を“数の式”に変える!
線分が等しい・正方形・対称・〇:□などの条件は、
そのままでは使えません。
必ず「長さ」や「高さ」の式にして整理するのがコツです。
💬 例)
- 「線分が等しい」→ 長さの式が等しい
- 「正方形」→ 縦の長さ = 横の長さ
- 「対称」→ x の符号を逆にする(y は同じ)
✅ ③ グラフは“描くため”じゃなく“考えるため”に使う!
放物線のグラフは、答えを出すための絵ではなく、
考えを整理するためのツール です。
頭の中で整理してから描くと、
どこに点があるのか・どんな形になっているのかが自然に見えてきます。
💡 慣れてきたら、頭の中で放物線をイメージできるようになろう!
✅ ④ 対称な点は “x の符号だけ反対”!
放物線は y軸対称です。
y の値は同じままで、x の符号だけを反転させればOK。
📍 例)
B(6, 12) → 対称な点A(−6, 12)
これを覚えるだけで、座標の整理が一気にスムーズになります。
✅ ⑤ 式と図を行ったり来たりする!
図形の問題は、式だけで突き進もうとすると迷子になります。
逆に図だけで考えると、正確さが失われます。
だからこそ、
「式で整理 → 図で確認 → 式で決定」
という“行ったり来たりの思考”が一番強い!
👧 あかり:「図と式、両方を使えるのが“本当の理解”なんだよ!」
💬 最後にひとこと
👦 ゆうと:「難しいと思ってたけど、やることは“座標・対称・式”の3つだけなんだね!」
👧 あかり:「そう!形を数字で整理できれば、どんな問題も解けるようになるよ✨」
🧮 確認問題(放物線×図形編)
【問題①】放物線 y=1/2x² 上に点A(4, a) がある。
この放物線と y軸対称 の位置に点Bがあるとき、点Bの座標を求めよ。
🧩 解説
点Aが \( y = \frac{1}{2}x^2 \)上にあるので、
A(4, a) の y 座標を求める:\( a = \frac{1}{2}(4)^2 だからa = 8 \)
よって A(4, 8)。
y軸対称なので、x の符号を反対にするだけ。
B(−4, 8) が答え。
💡ポイント: y軸対称 → x の符号だけ反転、y は同じ。
【問題②】 放物線① y=1/3x² と、放物線② y=ax² がある。
x軸に平行な直線 y=12が、放物線①と②をそれぞれ2点ずつで交わる。
放物線①との交点の1つが B(6, 12) のとき、
放物線②との交点のうち、x が正の方の点D の座標と、a の値を求めよ。
🧩 解説
放物線①にB(6, 12)がある。点Aと点Bは、y軸対称なので、A(−6, 12)。
よって、AB の長さ=12。
直線上で AB が12、AC=CD=DB の3等分とすると、1区間=4
よってB(6,12) から左に4進むと D(2,12)。
D は放物線②上の点なので、\( 12 = a×(2)^2 だからa = 3 \)
💡ポイント:
放物線が複数出たら、まず交点の座標を整理!
あとは文字aを式に代入して解くだけ。
【問題③】放物線 y=1/4x² と y=ax² がある。
点A(2, 1) は前者の上にあり、点D(2, 4a) は後者の上にある。
この2つの放物線上に点A, B, C, D をとって 四角形ABCDが正方形 になるとき、
a の値を求めよ。
🧩 解説: A(2,1)、y軸対称の位置にB(−2,1)。
Aの真下にD(2, 4a)、Dとy軸対称の位置にC(−2, 4a)。
正方形の条件:
AB(横の長さ)=AD(縦の長さ)
AB=Aのx座標-Bのx座標=2-(-2)=4
AD=Aのy座標-Dのy座標=1-(4a)=1 − 4a
したがって,1-4a-4
-4a=3
\( a = -\frac{3}{4}\)
💡ポイント:
正方形条件 → 横=縦。
図形条件を「式」に直して a を求めるのがコツ。
🚀 「その手応え、間違いなく本物だ!」
✨ここまで読んだ君は、もう「考える力」が確実に伸びています。
次に進む準備は、もうできている。
最近、ちょっと“できるかも”って感じてきた?
それ、偶然じゃないよ。
君が積み上げてきた時間と考えた回数が、確実に形になってるんだ。
👦 ゆうと:「前より早く解けるようになってる!」
👧 あかり:「それって、考え方が“自分の中に染み込んできた”ってことだよ!」
もう君は、“わかるようになりたい人”じゃなくて、
“わかるようになってきた人”なんだ。
いいぞ、いいぞ!
この調子でいけば、他の子たちより一歩も二歩も先を走れる。
あとは、この流れを止めないこと。
できるようになってきた自分を信じよう!理解の貯金は確実に増えてる。
🚀 この勢いで、次の問題へ!










