🧩相似と平行線の比の使い分け
👦ゆうと:「うわっ、この2つの問題、形は似てるのに解き方が違うんだね。どっちも線がいっぱいあるけど、どう見分けたらいいの?」
👧あかり:「いい質問だね! ポイントは、“どの線の長さを聞かれているか”なんだよ。」
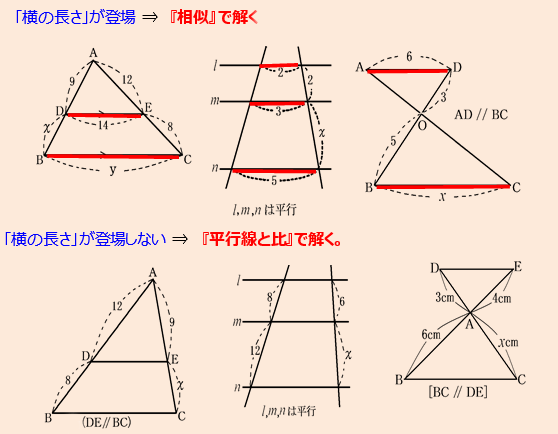
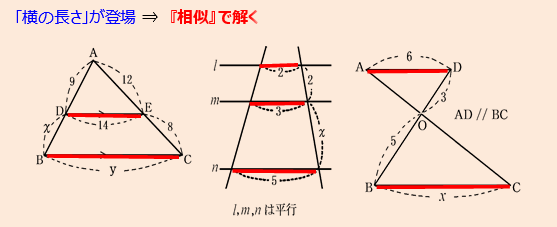
①「横の長さ」を聞かれたら ⇒ 『相似』で解く!
👧あかり:「図を見てみよう。どれも“横の線”の長さ(赤い線)を求める問題になってるよね。
こういうときは、“相似の三角形”を見つけて、その相似比を使って考えるんだ。」
👦ゆうと:「相似比って、上の三角形と下の三角形の比ってこと?」
👧あかり:「そう! しかもここが大事!
“相似”を使うときの比は、三角形どうしで比をとるから、
上の三角形の辺と下の三角形の辺を対応させて、
上の三角形の長さ:下の三角形の長さという形で比をとるんだよ。
だから、“下の三角形は三角形全体でとる”ことを忘れちゃダメ!」
👦ゆうと:「なるほど。途中の線までで止めちゃうと、全体の相似比にならないんだね。
上の段の左の図の場合だと、12:8じゃなくて、12:20にするってことだよね。」
👧あかり:「その通り! “横を聞かれたら、三角形の相似比”を意識してね。
比は12:20=3:5だから、3:5=14:y で、y=35cmだね。」
👦ゆうと:「OK!ばっちりだよ。」
👧あかり:「ちなみに、上の2つの図は見た目は違うけど、
縦の線を右や左に平行移動すると、実はどれも同じ構造なんだよ。」
👦ゆうと:「えっ? どういうこと?」
👧あかり:「例えば、真ん中の図の場合、左側の縦の線を右に2cm平行移動すると、左の図と同じ形になるでしょ。」
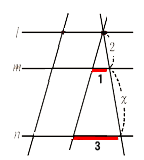
👦ゆうと:「あっ、なるほど!すごいね。
右に2cm平行移動すると、間の長さは上から0、1、3cmになるから、相似比は1:3になるわけだ。
だから、1:3=2:xで解けるね。」
👧あかり:「少し違うよ。“下の三角形は三角形全体でとる”ことを忘れちゃダメ!」
👦ゆうと:「あ~、そうか。じゃあ、1:3=2:(2+x) だね。だから x=4cm。」
👧あかり:「その通り!最後の右の図も同じ考え方だよ。」
👦ゆうと:「これは簡単だね。三角形の相似比は3:5だから、3:5=6:x で x=10cm!」
🟢先生コメント
👨🏫先生:「とてもいいね。上の3つの図は見た目が違っても、どれも“横の長さを求める相似の問題”なんだ。
つまり、“下の三角形は全体でとる”というルールさえまもれば、どんな形でも同じ方法で解けるぞ!」
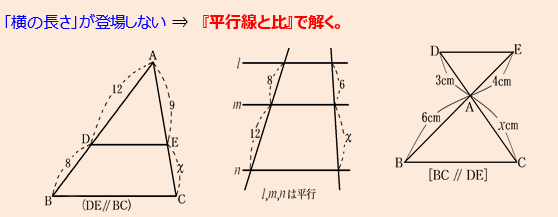
②「縦の長さ」を聞かれたら ⇒ 『平行線と比』で解く!
👦ゆうと:「じゃあ、下の段の図は“縦の長さ”を求める問題だね。」
👧あかり:「そうそう! このときは“平行線と比”を使うんだ。
ポイントは、右側の線の上対下=左側の線の上対下 という関係を使うこと!」
👦ゆうと:「えっ、三角形の相似じゃないの?」
👧あかり:「違うの。
平行線があると、縦の線分が同じ比で分けられるから、
三角形を作らなくても、上対下=上対下 という形で直接、比を立てられるんだよ。
これが“平行線と比”の考え方なんだ。」
👦ゆうと:「便利だね。相似のときは“上の三角形対下の三角形”、
平行線のときは“右の線の上対下=左の線の上対下”なんだね!」
👧あかり:「その通り!」
👦ゆうと:「じゃあやってみるね。
左の図は 12:8=9:x → x=6cm。
真ん中は 8:12=6:x → x=9cm。
右は 3:6=4:x → x=8cm。どう、全部あってる?」
👧あかり:「右だけ違うよ。
“上対下=上対下”っていうのは、1本の線の中での上対下のこと。
途中で曲がったり交わったりしても、同じ縦の線を上から下まで追いかけるんだよ。」
👦ゆうと:「なるほど。じゃあ 3:x=4:6 だね。だから x=4.5cm!」
👧あかり:「正解!
“縦の長さを聞かれたら平行線と比、横の長さを聞かれたら相似比”。
この区別ができると、似た形の図でもスッと判断できるようになるよ。」
💡まとめ
👨🏫先生:「同じような図に見えても、どの長さを聞かれているかで解き方が変わるんだ。
- 横の長さ → 三角形どうしで比をとる『相似』
- 縦の長さ → 平行線の間で上対下をとる『平行線と比』
見た目で迷ったら、“聞かれている線が横か縦か”をまずチェック!
“横=相似”、“縦=平行線と比”――この判断ができればもう完璧だ!」
👦ゆうと:「うん、これなら迷わず選べそう!」
🎯先生から「ここだけは絶対押さえろ!」
👨🏫「みんな、ここが今日の一番大事なポイントだよ。
“相似”と“平行線と比”は、どっちも『比』を使うけど、比のとり方がまったく違うんだ。
この違いが分かれば、どっちを使うかで迷わなくなるぞ!」
① 横の長さを聞かれたら → 『相似』で解く!
👨🏫「“横の線”の長さを求めるときは、三角形どうしが相似になるところを使って考える。
このときの比は、上の三角形:下の三角形 のように、
“三角形全体の辺どうし”で比をとるんだぞ。」
👨🏫「ここを間違える子が多い!
途中の線だけで比をとると、全体の相似比がズレてしまう。
だから“下の三角形は上から下まで、全部の長さでとる”ことを忘れないように!」
👨🏫:「見た目が違っても、上の段の3つの図は実は同じ構造なんだ。
たとえば縦の線を右や左に平行移動してみると、
“重なり方”が違うだけで、同じ相似の関係になっている。
つまり、どの図も考え方はまったく同じ! だから、
“横を聞かれたら相似”と判断すれば全部片づくぞ。」
🟨② 縦の長さを聞かれたら → 『平行線と比』で解く!
👨🏫:「“縦の線”を求めるときは、“平行線の間の比”を使うんだ。
ここでは、右の線の上対下=左の線の上対下 という関係が成り立つ。
つまり、三角形を作らなくても、縦の線だけで比を立てられるってわけだ。」
👨🏫先生:「そしてこれも、“下の段の3つの図”は見た目が違っても、全部同じ構造なんだ。
縦の線を左右に平行移動すると、形は変わっても比の関係はまったく同じになる。
つまり、“縦を聞かれたら平行線と比”というルールで、どの図も同じように解けるんだ!」
💡まとめ
| 聞かれている長さ | 使う考え方 | 比のとり方 |
|---|---|---|
| 横の長さ | 相似の三角形 | 上の三角形の辺 : 下の三角形の辺(全体でとる) |
| 縦の長さ | 平行線と比 | 右の線の上対下 = 左の線の上対下 |
👨🏫:「つまり、“見た目が違っても同じ構造”ということを見抜くのがコツ!
横なら『相似比』、縦なら『平行線と比』。
聞かれている線が“横”か“縦”かで、どちらを使うか瞬時に判断できるようにしよう!」
🟨練習問題 「平行線と比」か「相似比」か。どっちを使う。
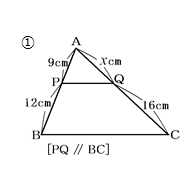
① 図のxを求めなさい。

👦ゆうと:「xは縦にあるから、「平行線と比」を使うよ。使い方は、右側の上:下=左側の上:下。
だから、 9:12=x:16で
x=12cm。」
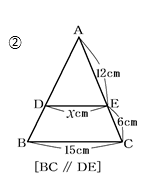
② 図のxを求めなさい。

👦ゆうと:「xは横にあるから、「相似比」を使うよ。上の三角形と下の三角形の相似比だから、
12:12+6で、カンタンにすると2:3。
下の三角形だから、6だけじゃなくて、12+6にすることを忘れちゃだめだよ。
2:3=x:15 だから、 x=10cm。」
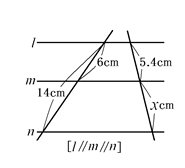
③ 図のxを求めなさい。

👦ゆうと:「これは、xが縦にあるから、「平行線と比」を使う。
左側の上:下は6:8だからカンタンにして、3:4。
だから、右側の上:下=左側の上:下は、3:4=5.4:x
x=7.2cm。」
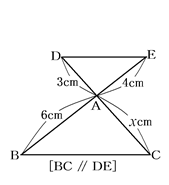
④ 図のxを求めなさい。

👦ゆうと:「これもxが縦にあるから、「平行線と比」だね。
DCは3:xで、EBは4:6だから、3:x=4:6
これを解いて、x=4.5cm。
2本の線が交わっていても、1本の線の上:下ともう1本の線の上:下を比べる点に注意してやれば大丈夫だよ。」