---

中3数学 ストーリーシリーズ

中3数学｜放物線と直線を座標で整理！図形を数字でとらえる二次関数の考え方（座標で考える第3弾）

放物線×直線の交点・等積変形・中点を“数字で見える化”。ストーリーでスッと腑に落ちる入試頻出テーマを攻略！

🎬 ゆうと＆あかりのストーリー解説

放物線と直線の出会いで生まれる三角形のナゾを解け！（座標で考える第3弾）

---

🧩 問題設定

放物線 \( y = ax^2 \) と直線 \( y = x + 4 \) が交わってできる図形を考える。
この2つの交点をそれぞれ \( A \)、\( B \) とし、原点を \( O(0,0) \) とする。 以下の3つの問いに答えよう。

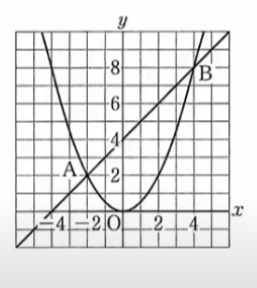
1️⃣ 放物線の係数 a の値を求めよ。
2️⃣ 点 P が放物線上を A から B まで動くとき、
　　三角形 △AOB と △APB の面積が等しくなる点 P の座標を求めよ。
3️⃣ 原点 O を通り、三角形 △AOB の面積を2等分する直線の式を求めよ。

---

👦 ゆうと：
「また三角形の面積？しかも放物線と直線が関係してるって…もう混乱しそうなんだけど。」

👧 あかり：
「大丈夫！　放物線と直線が作る三角形の座標で整理して考えれば大丈夫！」

---

① 放物線の形を決めよう！

👦 ゆうと：「放物線は \( y = ax^2 \)、直線は \( y = x + 4 \) か。\( a \) がわからないね。」

👧 あかり：「でも、グラフを見れば交点 \( B(4,8) \) がわかる。
この点は放物線の上にあるから、代入して \( a \) を求めよう！」

\( a \times 4^2 ＝8 \)
\( 16a = 8 \Rightarrow a = \frac{1}{2} \)

👦 ゆうと：「\( a = \frac{1}{2} \)！つまり、放物線の式は \( y = \frac{1}{2}x^2 \) だね。」

👧 あかり：「その通り！上に開くゆるやかな放物線になったね。」

---

② 面積が同じになる点Pを見つけよう！（等積変形の発想）

👦 ゆうと：「“△AOBと△APBの面積が等しい”って書いてあるけど…
どうやってそんな点Pを見つけるの？」

👧 あかり：「まず気づいてほしいのはね、どっちの三角形にもAとBが入ってること。」

👦 ゆうと：「あ、ほんとだ！じゃあ、底辺ABは共通なんだね。」

👧 あかり：「そう。つまり、△AOBから△APBに変わるってことは、
底辺ABはそのままで、点Oだけが動いて点Pになったって考えられるんだよ。
ここで“面積が等しい”ということは、高さが変わっていないということになるの。」

👦 ゆうと：「底辺が同じで高さが同じなら、確かに面積は同じだね！」

👧 あかり：「そこで出てくるのが“等積変形（とうせきへんけい）”。
これは、“底辺を固定して、もう1つの頂点を底辺に平行な線の上で動かすと、
三角形の面積は変わらない”という考え方なの。」

👦 ゆうと：「つまり、Oを通ってABに平行な線を引いて、Oがその線の上を動けば、
どこに動かしても面積は同じになるんだね！」

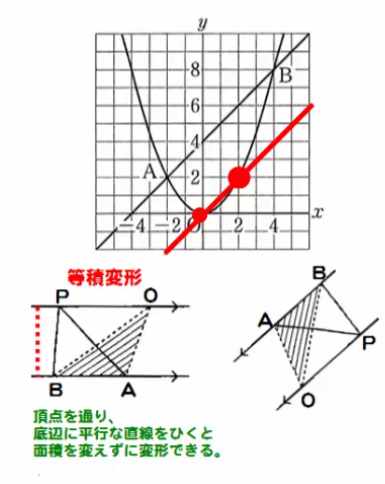
👧 あかり：「そう！そして今回の条件に“Pは放物線の上にある”と書いてある。
つまり、“放物線”と“ABに平行でOを通る直線”の交点を求めればいいの！」

👦 ゆうと：「ということは、まずOを通ってABに平行な線をだす。
ABの式が \( y = x + 4 \) だから、傾きは 1。
O を通って傾きが 1 の線は　→　 \( y = x \)。」

👧 あかり：「よし、放物線 \( y = \frac{1}{2}x^2 \) と連立してみよう！」

\( \frac{1}{2}x^2 = x \)

両辺を2倍して移行すると、\( x^2 – 2x = 0 \Rightarrow x(x – 2) = 0 \)

👦 ゆうと：「\( x = 0 \) と \( x = 2 \) が出た。
\( x = 0 \) は O だから、もう1つの点が \( P(2, 2) \) だね！」

👧 あかり：「その通り！
つまり、放物線の上でABに平行な線と交わる点P(2,2)。
そこが、△AOBと△APBの面積が等しくなる点なんだよ。」

👦 ゆうと：「“等積変形”って、動かしても面積が同じ！ってことなんだね。
なんか、図形が生きてるみたいだ！」

👧 あかり：「うん、“形を動かして考える”のが数学の面白さなんだよ。」

---

③ 面積を2等分する直線を求めよう！

👦 ゆうと：「最後は、△AOB の面積を 2 等分する直線を求めるんだね。
これも“動かす”発想でいけるの？」

👧 あかり：「うん。三角形の面積を 2 等分する直線は、“対辺の中点を通る”のが基本だよ。
どうしてかというと、三角形の頂点を通る線が対辺の中点を通ると、2 つの三角形はどちらも
底辺の長さが同じで、高さも共通になるから、面積が等しくなるの。」

👦 ゆうと：「なるほど！ 底辺が同じで高さが同じなら、面積も同じになるってことか！」

👧 あかり：「そういうこと！ じゃあ、△AOB の対辺 AB の中点を求めてみよう。」

👦 ゆうと：「A と B の座標は、A\( (-2, 2) \)、B\( (4, 8) \) だね。」

👧 あかり：「うん。中点というのは“真ん中の点”。真ん中ってことは、2つの点のちょうど平均になるんだ。
だから、x 座標どうしを足して 2 で割る、y 座標どうしを足して 2 で割るんだよ。」

👦 ゆうと：「平均ってことか！ じゃあ、計算してみよう。」

👧 あかり：「中点の座標は、
\( M\left( \frac{-2 + 4}{2}, \frac{2 + 8}{2} \right) = (1, 5) \) になるよ。」

👦 ゆうと：「ふむふむ、確かにどっちも“真ん中”って感じだね！」

👧 あかり：「次に、この中点 M と原点 O を通る直線を求めよう。」

👦 ゆうと：「原点 \( O(0, 0) \) と中点 \( M(1, 5) \) を通る直線の傾きは、\( \frac{5 – 0}{1 – 0} = 5 \)。
だから、直線の式は \( y = 5x \) だね！」

👦 ゆうと：「これで完成！ 三角形をちょうど 2 つに分ける線の式は \( y = 5x \)！」

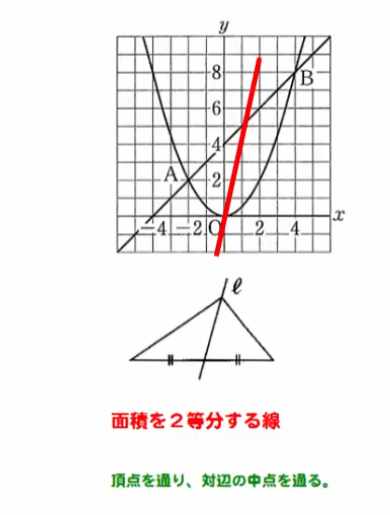
👧 あかり：「完璧！ “中点を通る”っていう発想と、“真ん中＝平均”の考え方は、図形問題の超基本テクニックなんだよ。」

👧 あかり：「次に、この中点 M と原点 O を通る直線を求めよう。」

👦 ゆうと：「原点 \( O(0, 0) \) と中点 \( M(1, 5) \) を通る直線の傾きは、\( \frac{5 – 0}{1 – 0} = 5 \)。
だから、直線の式は \( y = 5x \) だね！」

👦 ゆうと：「これで完成！ 三角形をちょうど 2 つに分ける線の式は \( y = 5x \)！」

👧 あかり：「完璧！ “中点を通る”っていう発想と、“真ん中＝平均”の考え方は、図形問題の超基本テクニックなんだよ。」

---

💡 あかりのまとめ

👧 あかり：「今回のポイントをまとめるね！」

1️⃣ 面積が等しいときは、“等積変形”を使う！
　　底辺を固定して、もう1つの頂点を平行に動かしても面積は同じ。
2️⃣ 面積を2等分する直線は、“対辺の中点を通る線”。

👦 ゆうと：「見た目の図形を座標を使って考えると、かなり簡単に見えてくるね！」

---

🎯 放物線×図形の考え方Q&A（ゆうと＆あかりの会話）

Q1. どうして放物線と直線の交点を見つけるの？

👦 ゆうと：「グラフを描かなくても、なんとなく形はイメージできるけど、どうして“交点”を求めるの？」
👧 あかり：「交点って、“2つの線が同じ高さでぶつかる場所”のことだよ。
だから、y の値が同じときの x を求めることで、線と線のつながりを数字で考えられるんだ。
交点を求めるのは、“図形を数字の世界に変える第一歩”なんだよ！」

💡 ポイント：交点を求める＝グラフを数字で考える準備！

Q2. どうして等積変形を使うと面積がすぐ出せるの？

👦 ゆうと：「さっきの等積変形ってすごいけど、どうして形を動かしても面積が変わらないの？」
👧 あかり：「いい質問！ 等積変形は、“底辺を動かさずに、もう一つの点を底辺に平行に動かす”って考え方なんだ。
底辺と高さが同じなら、三角形の面積も同じ。だから動かしても面積は変わらないんだよ。」

💡 ポイント：底辺と高さが同じ＝面積は同じ。これが等積変形の基本！

Q3. 中点を求めるとき、どうして2で割るの？

👦 ゆうと：「中点を出すとき、いつも“足して2で割る”ってやるけど、なんで2で割るの？」
👧 あかり：「中点は“真ん中の点”。真ん中っていうのは“平均”なんだよ。
たとえば、2人の身長が150cmと170cmだったら、その真ん中は(150+170)÷2=160でしょ？
だから座標も同じで、xどうし、yどうしを足して2で割れば真ん中＝中点になるの。」

💡 ポイント：中点＝2つの数の平均。足して2で割るだけ！

Q4. 面積を2等分する線が“中点を通る”ってどういうこと？

👦 ゆうと：「“面積を2等分する線は中点を通る”って言うけど、なんで？」
👧 あかり：「三角形を2つに分けたいとき、頂点から対辺の“ちょうど真ん中”を通る線を引けば、
2つの三角形の底辺が同じ長さで、高さも共通になるから、面積がピッタリ半分になるんだ。
これが“中点を通る”っていう意味だよ。」

💡 ポイント：頂点から対辺の真ん中を通れば、2つの面積は自動的に半分！

Q5. 図形の問題で迷ったとき、どこから考えればいいの？

👦 ゆうと：「問題が難しいと、どこから手をつけていいかわかんなくなるんだよね…。」
👧 あかり：「まずは、すべての点の座標を調べること。これは絶対。　
次は、“動かないもの”と“動くもの”を分けて考えるといいよ。
たとえば、原点や軸は動かない。放物線の形や点Pみたいに動くものは、その上で関係を作る。
“どれが固定で、どれが動くか”を整理すれば、混乱しないで考えられるんだ。」

💡 ポイント：まず“動かないもの”を見つける！そこが考える出発点。

🧑‍🏫ここだけは絶対に押さえろ！

確認問題　差がつく問題