中3理科 だんだん速くなる運動とは|等加速度運動と時間²に比例する距離の仕組みをやさしく解説【自由落下の例も】
1. だんだん速くなる運動(等加速度運動)とは?|毎秒同じだけ速さが増える運動
👦 ゆうと:「あかり、質問! “だんだん速くなる運動”ってどういうこと?」
👧 あかり:「いいね!それは“等加速度運動”のこと。教科書では“だんだん速くなる運動”って書かれているね。簡単にいうと、毎秒同じだけ速さが増えていく運動のことだよ。」
👦 ゆうと:「ふむふむ…でも、“毎秒同じだけ速さが増える”って、距離で考えるとどうなるの?」
👧 あかり:「いい質問だね!じゃあ実際に、1秒ごとの進んだ距離を足してみて、確かめてみよう。」
中3理科 方法A:1秒ごとの距離を足してみよう|等加速度運動の合計距離の求め方をやさしく解説
2. 方法A|1秒ごとの距離を足して確認!等加速度運動の合計距離の出し方
👦 ゆうと:「じゃあ…
1秒まで → 速さは0m/秒から10m/秒に変わるから、平均は5m/秒で、1秒で → 5×1=5m進む。
2秒まで → 速さは0m/秒から20m/秒に変わるから、平均は10m/秒で、2秒で → 10×2=20m進む。
3秒まで → 速さは0m/秒から30m/秒に変わるから、平均は15m/秒で、3秒で → 15×3=45m進む。
4秒まで → 速さは0m/秒から40m/秒に変わるから、平均は20m/秒で、4秒で → 20×4=80m進む。
こうして計算すればいいんだ!」
👧 あかり:「そうそう!1秒で5m、2秒までで20m、3秒までで45m、4秒までで80m進むでしょ。」
📊 対応表でまとめると…
| 時間(秒) | 平均の速さ | 合計距離(m) | 別の考え方 |
|---|---|---|---|
| 0秒 | 0 | 0 | |
| 1秒 | (0+10)÷2=5 | 5 (5×1) | 5×1² = 5 |
| 2秒 | (0+20)÷2=10 | 20 (10×2) | 5×2² = 20 |
| 3秒 | (0+30)÷2=15 | 45 (15×3) | 5×3² = 45 |
| 4秒 | (0+40)÷2=20 | 80 (20×4) | 5×4² = 80 |
👧 あかり:「いいね!つまり『平均の速さ × 時間』で、その時点までの距離が出せるんだよ。そして表に一番右を見て!その結果は『5×時間²』っていう形になっているの。」
👦 ゆうと:「え~ ほんとだ!合計は全部“5×時間²”になってる!」
👧 あかり:「つまり、進んだ距離は時間の2乗に比例するんだよ。」
中3理科 方法B:グラフで確かめよう|v-tグラフで面積から距離を求める仕組みをやさしく解説
3. 方法B|v–tグラフで理解する 等加速度運動と距離の関係
👦 ゆうと:「でも、なんで時間²になるの?」
👧 あかり:「じゃあグラフで見てみよう。速さを縦、時間を横にしたグラフを考えるよ。」
1秒 → 速さ10m/s
2秒 → 速さ20m/s
3秒 → 速さ30m/s
4秒 → 速さ40m/s
👧 あかり:「この点をつなぐと右上がりの直線になるんだ。そして距離はこの直線と横軸に囲まれた三角形の面積で表せるよ。」
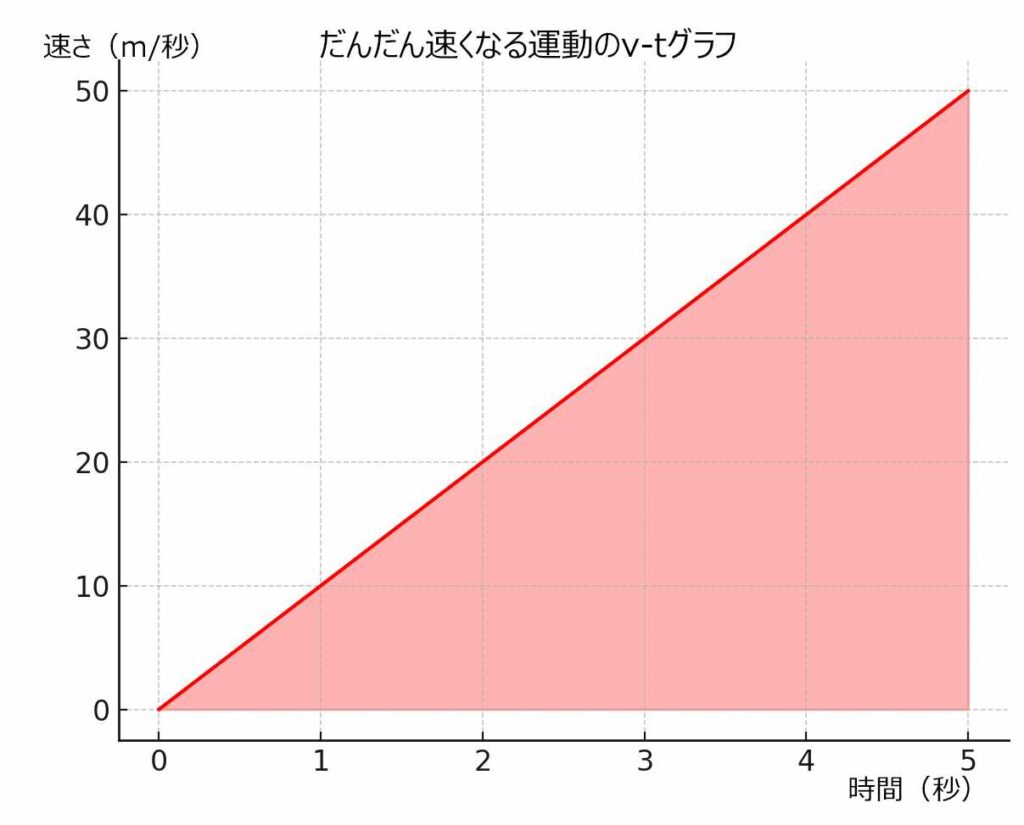
👦 ゆうと:「三角形の面積が距離?」
👧 あかり:「そう。数字で確認してみよう。単位にも注目してね。
- 2秒まで → 底辺2秒 × 高さ20cm/秒 ÷ 2 = 20cm
- 3秒まで → 底辺3秒 × 高さ30cm/秒 ÷ 2 = 45cm
- 4秒まで → 底辺4秒 × 高さ40cm/秒 ÷ 2 = 80cm
ね、表の合計距離とピッタリ一致するでしょ?」
👦 ゆうと:「本当だ。 すげ~。 三角形の面積が移動距離になるんだ!」
👧 あかり:「しかも、三角形の面積の式は 底辺×高さ÷2。ここで底辺=時間、高さ=速さ=10×時間だから、
底辺×高さ÷2=時間×(10×時間)÷2=5×時間² になるの。
だから “距離は時間の二乗に比例する” って結論にたどり着けるんだよ。」
👦 ゆうと:「なるほど!すごいね。面積の式から“時間²”が自然に出てくるんだ!やっと納得できた!」
👧 あかり:「うん。これが“だんだん速くなる運動”の大事なポイント。数字でも、グラフでも、式でも同じことを言ってるんだよ。」
中3理科 方法C:公式を使ってみよう|時間の二乗と距離の関係を公式で理解する
4. 方法C|s–tグラフが曲線になる理由|距離が時間²に比例する仕組み
方法Cに入る前の確認
👦 ゆうと:「じゃあ次! 距離–時間(s–t)グラフは、なんで直線じゃなくて曲線になるの?」
👧 あかり:「それを確認するために、もう一度“合計距離”を見直してみよう。」
- 0秒 → 0m
- 1秒 → 5m
- 2秒 → 20m
- 3秒 → 45m
- 4秒 → 80m
👦 ゆうと:「ふーん…。ここから何がわかるの?」
👧 あかり:「じゃあ“どれくらい増えたか”を表にしてみよう。」
| 時間(秒) | 合計距離(m) | どれくらい増えたか(m) |
|---|---|---|
| 0秒 | 0m | – |
| 1秒 | 5m | +5m |
| 2秒 | 20m | +15m |
| 3秒 | 45m | +25m |
| 4秒 | 80m | +35m |
👧 あかり:「見て。差が 5 → 15 → 25 → 35 って、毎回10ずつ大きくなってるよね?」
👦 ゆうと:「あ、そうか!増え方が 5 → 15 → 25 → 35ってどんどん大きくなるから、まっすぐじゃなくて曲線になるんだ!」
👧 あかり:「さらに“2倍→4倍チェック”もできるよ。2秒で20m、4秒で80m。時間が2倍で距離は4倍になってるでしょ?」
👦 ゆうと:「ホントだ!時間²に比例してるんだ!」
方法Cの結論
👧 あかり:「だからs–tグラフは“二次関数のカーブ”になるんだよ。時間が進むほど、増え方がだんだん大きくなっていく形になるんだ。」
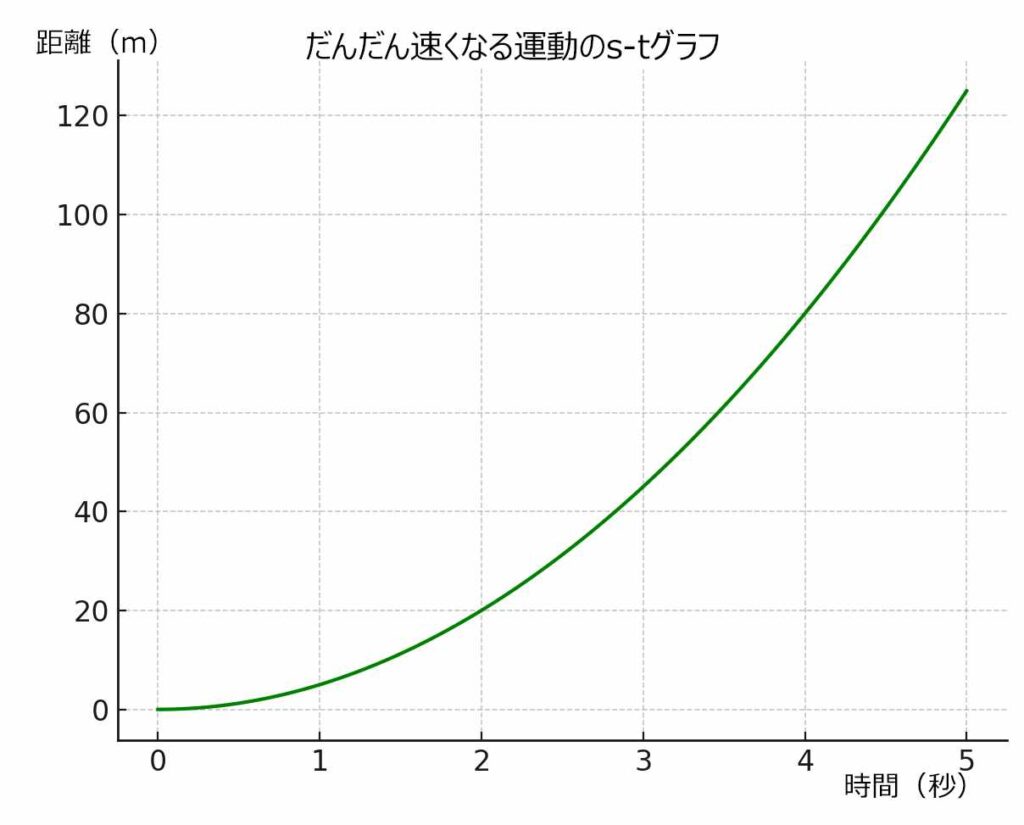
👦 ゆうと:「v–tグラフでは面積=距離、s–tグラフは二次関数で、距離は時間²に比例だね!」
👧 あかり:「そう!これで“だんだん速くなる運動”がどう表せるか、数字でもグラフでもバッチリ分かったでしょ!」
中3理科 力との関係も押さえよう|一定の力が働くと速さや運動がどう変化するかを解説
5. 力との関係も押さえよう|一定の力と等加速度運動(自由落下の例)
👧 あかり:「ところで、この“だんだん速くなる運動”はどうして起こるか知ってる?」
👦 ゆうと:「うーん…。」
👧 あかり:「これはね、一定の力がずっと加わっているからなんだよ。
たとえば“自由落下”もそう。重力という一定の力が働き続けるから、速さがどんどん増えていくんだ。」
👦 ゆうと:「なるほど!」
👧 あかり:「逆にね、坂道を上る運動や、自転車でブレーキをかけるときは、進む向きと逆向きに一定の力が働く。だから“だんだん遅くなって止まる”んだよ。」
👦 ゆうと:「あ、そっか!ぼく、“力が大きくなるから、だんだん速くなる”って思ってたけど、それは間違いなんだね。進む向きに一定にの同じ力が働けば、だんだん速くなり、逆向きならだんだん遅くなるんだ!わかったぞ。」
👧 あかり:「その通り!“一定の力”がどちら向きに働くかで、だんだん速くなるか、だんだん遅くなるかが決まるんだよ。」
6. だんだん速くなる運動のQ&A|よくある疑問と解説まとめ
- Q1 👦 ゆうと:「どうして“だんだん速くなる運動”では、進んだ距離が“時間²”に比例するの?」
-
👧 あかり:「1秒ごとの“増え方”を見てみて。5 → 15 → 25 → 35…って毎回10ずつ大きくなってるよね。つまり“増え方が増えている”から、まっすぐじゃなく曲線になる。だから時間²に比例するんだよ。」
- Q2 👦 ゆうと:「v–t(速さ–時間)グラフで、どうして面積が“距離”になるの?」
-
👧 あかり:「いい質問だね!“速さ×時間=距離”だからなんだよ。
たとえば速さがずっと同じなら、グラフは横にのびた“長方形”になって、その面積が“速さ×時間”になるんだ。
でも“だんだん速くなる運動”のときは速さが増えていくから、グラフは右上がりの直線になる。その下にできるのは“三角形”。
だから三角形の面積=底辺(時間)×高さ(速さ)÷2 が、そのまま進んだ距離になるんだよ。」
- Q3 👦 ゆうと:「2秒で20m、4秒で80m。なんで時間が2倍になると距離は4倍になるの?」
-
👧 あかり:「これは“時間²”の特徴。2²=4、4²=16だから、時間を2倍にすると2²→4²で4倍になるんだ。」
- Q4 👦 ゆうと:「どうして速さが“毎秒同じだけ”増える運動になるの?」
-
👧 あかり:「それは一定の力がずっと働き続けているから。力が一定だと、速さの増え方(加速度)も一定になるんだよ。」
- Q5 👦 ゆうと:「じゃあ、一定の力が逆向きに働くとどうなるの?」
-
👧 あかり:「進む向きと逆向きの力なら、ブレーキになるよ。自転車でブレーキをかけると、だんだん速さが小さくなって止まるのと同じだね。」
中3理科 だんだん速くなる運動のまとめ|ここだけは押さえる重要ポイント
📌 だんだん速くなる運動(等加速度運動)のポイント
一定の力が働き続けると、 だんだん速くなる運動になる
例:自由落下では、重力という一定の力でだんだん速くなる。
逆に:坂を上る運動や自転車のブレーキは、進行方向と逆向きの一定の力で、だんだん遅くなり、やがて止まる。
斜面上の物体.jpg)
距離は時間²に比例する
1秒で5m、2秒で20m、3秒で45m、4秒で80m。
こうして「合計距離=5×時間²」という形になる。
👉 時間を2倍にすると、距離は4倍になるのが大きな特徴。
v–tグラフでは「面積=距離」
縦が速さ、横が時間。
だから面積=縦×横=速さ×時間=距離になる。
👉 グラフを使うと「時間²の関係」が数字ではっきり見える。
s–tグラフは二次関数のカーブ
距離の増え方が「5→15→25→35」と毎回大きくなるから、直線ではなくだんだん急になる曲線になる。
等加速度直線運動のグラフ.jpg)
中3理科 だんだん速くなる運動のまとめテスト|基礎確認の一問一答
7.📝 確認問題(だんだん速くなる運動)|基礎から入試対策まで
① だんだん速くなる運動(等加速度運動)とは、どんな運動ですか?
👉 答: 毎秒同じだけ速さが増えていく運動。
👉 解説: 「等加速度運動」は速さの増え方が一定の運動をさす。教科書では「だんだん速くなる運動」と説明される。
② 速さが毎秒10m/sずつ増える運動で、2秒までに進んだ距離は?
👉 答: 20m
👉 解説: 0秒から2秒までの平均の速さは10m/s。 平均の速さ10 × 時間2秒 = 20m。
別の考え方では「5×2²=20m」と表せる。
ここで出てくる「5」は、速さの増え方(毎秒10)の半分。
なぜなら速さが0から20まで直線的に増えるから、平均はちょうど半分の10になる。
その「半分」が式に反映されて「5×時間²」になる。
③ v–t(速さ–時間)グラフでは、面積は何を表しますか?
👉 答: 進んだ距離
👉 解説: 縦=速さ、横=時間だから、面積=速さ×時間=距離。
④ s–t(距離–時間)グラフは直線になりますか?曲線になりますか?その理由も答えなさい。
👉 答: 曲線になる。
👉 解説: 毎秒の増え方が5→15→25→35と大きくなるため、直線ではなく「だんだん急になる曲線(=二次関数の形)」になる。
⑤ 一定の力が働き続けると、物体の運動はどうなりますか?例を1つ答えなさい。
👉 答: だんだん速くなる運動(等加速度運動)になる。例:自由落下。
👉 解説: 一定の力(重力など)が加わり続けると、速さが毎秒同じだけ増える。逆にブレーキのように逆向きの一定の力が加わると、だんだん遅くなって止まる。
8.📝 まとめテスト(だんだん速くなる運動)|記録タイマー・自由落下の応用問題
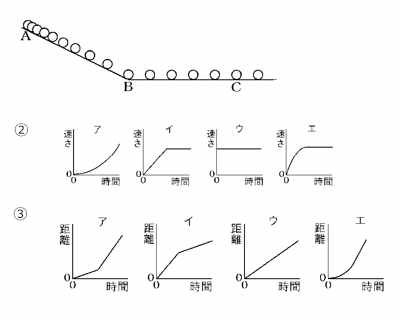
問題1 なめらかな斜面の上から小球を転がした。図は0.1秒ごとの位置を記録したものである。
摩擦はなく、球は直線的に進む。
① 斜面を下った後、水平部分BCでは速さはどうなるか。
ア. 速さは増える イ. 速さは一定 ウ. 速さは減る エ. ゆっくり加速する
② A~B~Cまでの速さと時間の関係を表すグラフとして正しいものを選べ。
③ A~B~Cまでの距離と時間の関係を表すグラフとして正しいものを選べ。

① ア
BC間では位置の間隔が等しいので、速さが一定。→ 等速直線運動している。
② イ
斜面を下るAB間はだんだん速くなり、水平面のBC間は等速直線運動。
③ エ
斜面を下るAB間は、距離は時間の2乗に比例。水平面のBC間は、距離は時間比例。
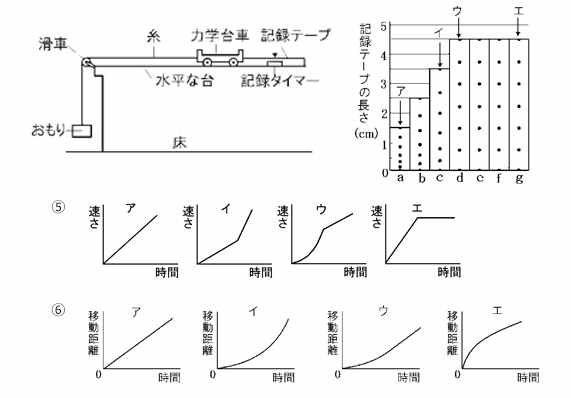
問題2 小さなおもりで台車を引っ張り、記録タイマーで動きを測定した。おもりが床に着くと糸が切れ、その後は摩擦なく動く。記録タイマーは1秒間に60打点する。記録テープは6打点ごとに区切り貼り付けた。
① 記録点の間隔を利用して、記録テープgの台車の平均の速さを求めよ。
② おもりが床に到達したのは、A~エのどの部分か答えよ。
③ おもりが落ちている間に台車に働く力の特徴はどれか。
ア. 時間とともに増える イ. ゼロ ウ. 一定 エ. 減少する
④ 糸が切れた後の台車の運動は何か。
⑤ a〜gまでの運動のv–tグラフとして正しいものを選べ。
⑥ a〜gまでの運動のs–tグラフとして正しいものを選べ。

① 45 cm/秒
記録テープgは0.1秒で4.5cmだから、4.5÷0.1=45cm/秒。
② イ
おもりが床に着くと引く力が0になるから 等速運動に変わる。→ 打点間隔が等しくなるところ。
③ ウ
台車を引く力は、重力がおもりを引く力で、つねに一定。
④ 等速直線運動
おもりがなくなった後は力がゼロなので等速運動。
⑤ エ
a~c間はだんだん速くなる運動。c~gは等速直線運動。
⑥ ウ
a~c間は2次関数の放物線。c~gは1次関数の直線。
中3理科 だんだん速くなる運動の勉強を頑張った君へ|激励メッセージ
9. 🌟 読んでくれた君へ、激励メッセージ|難しい単元を乗り越えた君へ
🌟 ここまで本当によく頑張ったね!
「だんだん速くなる運動」は中学理科でも特に難しいところ。
でも、ここまで読みきった君は、すでに大きな山をひとつ登りきったんだ。
わからないと感じても大丈夫。理解しようと挑戦したその姿勢が、君の力になっているんだよ。
だから胸を張っていいんだ。
✨ 君なら絶対にできる!
この頑張りを続けていけば、きっと自信が持って解ける。