🎬 ゆうと&あかりのストーリー解説
放物線と直線の交点、そして三角形の面積!
🟣 導入
👦 ゆうと:「ねえあかり、放物線と直線の交点って、どうやって求めるの?
グラフで見れば交わってるのはわかるけど、座標が全然わからないんだよね。」
👧 あかり:「いいよ。交点っていうのは、“放物線と直線がちょうど同じ高さ(=yの値)でぶつかる場所”のことなんだ。
つまり、2つの式でyが同じになるときのxを見つければいいんだよ。」
👦 ゆうと:「あ、なるほど。
同じ高さのところを探すから、“yをそろえてxを求める”ってことか。」
👧 あかり:「そう!だから、連立方程式にして“同じyのときのx”を探すんだ。」
① 交点の座標を求めよう
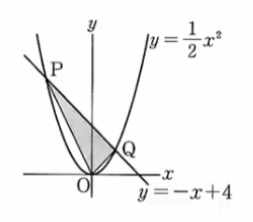
👧 あかり:「今回の問題は、放物線 \( y = \frac{1}{2}x^2 \) と直線 \( y = -x + 4 \) 。
同じ y のときに交わるから、こうやってくっつけるよ:
\[ \frac{1}{2}x^2 = -x + 4 \]
👦 ゆうと:「yが同じ高さだから、イコールでつなげるんだね!」
👧 あかり:「うん。分数があると面倒だから、両辺を2倍しよう。」
あかり:「右辺を左に移して2倍すると──」
\( x^2 = -2x + 8 \)
👧 あかり:「右辺を左に移して整理すると──」
\( x^2 + 2x – 8 = 0 \)
👦 ゆうと:「出た!二次方程式!」
👧 あかり:「これを因数分解すると、
\( (x + 4)(x – 2) = 0 \)
だから、\( x = -4 \) と \( x = 2 \) になるね。」
👦 ゆうと:「よし、xが2つ出た!」
👧 あかり:「この x を直線の式 \( y = -x + 4 \) に代入して、y を出してみよう。」
\( x = -4 \) のとき → \( y = -(-4) + 4 = 8 \)
\( x = 2 \) のとき → \( y = -(2) + 4 = 2 \)
👧 あかり:「だから、交点は P(-4, 8) と Q(2, 2)!」

👦 ゆうと:「おおっ!これが交点の座標か!」
👧 あかり:「そう、“yが同じときのx”を探す=連立する理由なんだよ。」
② △POQ の面積を求めよう
👦 ゆうと:「でも、次の『△POQの面積』ってどうやって出すの?」
👧 あかり:「これはね、ちょっとしたコツがあるよ。
まず、Oは原点(0,0)だから、y軸で左右に分けて考えるとわかりやすいの。」
👦 ゆうと:「y軸で分けるってどういうこと?」
👧 あかり:「直線 y=−x+4がy軸と交わる点はR(0,4)。
y軸を使って、三角形△POQを左の△PORと右の△QORの2つに分けるの。」
👦 ゆうと:「なるほど、真ん中で2つの三角形にするんだね。」
左側の△POR
👧 あかり:「まず、左側の△PORを見てみよう。
底辺はOR(長さ4)になるよね。」
👦 ゆうと:「じゃあ、高さは?」
👧 あかり:「高さは底辺ORに直角の距離、つまりP(-4,8)からy軸までの横の距離。
xが−4だから、高さは4。」
👦 ゆうと:「あ、長さだから、4 ってことか。
だから面積は \( \frac{1}{2} \times 4 \times 4 = 8 \) !」
👧 あかり:「正解!△PORの面積は8だね。」
右側の△QOR
👧 あかり:「次は右側の△QOR。底辺は同じOR=4。
高さはQ(2,2)からy軸までの横の長さだから2だよ。」
👦 ゆうと:「だから面積は \( \frac{1}{2} \times 4 \times 2 = 4 \) だね!」
👧 あかり:「うん、よくできた!
そして2つの三角形を足せば、△POQの面積になる。」 8+4=12
👦 ゆうと:「つまり、△POQ の面積は 12!」
👧 あかり:「その通り!
この“y軸で分けて考える”方法が一番わかりやすいんだ。」
③ 発展編:等積変形で一気に出す方法
👦 ゆうと:「でも、2つに分けて足すのって、ちょっと手間がかかるね。」
👧 あかり:「そうだね。
そこで使えるのが、“等積変形”っていう考え方なんだ。」
👦 ゆうと:「どういうこと?」
👧 あかり:「まず、さっきと同じようにy軸で左右に分けるよ。
左は△POR、右は△QOR。
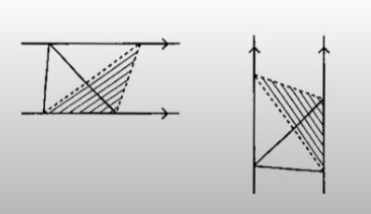
ここから、それぞれの三角形を“平行線を使って”動かしてみよう。」
左側の△POR → △TOR
👧 あかり:「点Pを通ってy軸に平行な線を引くと、その線はx軸と交わるね。
その交点をTとするよ。
これで、△PORが△TORに変わったよ。」
👦 ゆうと:「Pが下にスライドしてTになったんだね。」
👧 あかり:「うん。底辺ORは変わらないし、平行線の間が高さだから、高さも変わらない。
だから△PORと△TORの面積はまったく同じなんだ。」
👦 ゆうと:「え~、すごいね。これとううせき~。だんだっけ?。」
👧 あかり:「とうせきへんけい“等積変形”だよ。」
右側の△QOR → △SOR
👧 あかり:「右側もおなじようにするよ。点Qを通ってy軸に平行な線を引いて、x軸と交わる点Sをつくる。
△QORは、動いた形として△SORになる。」
👦 ゆうと:「僕がいってみるよ。点Qを通ってy軸に平行な線を引いて、x軸と交わった点をSとする。
△QORと△SORは、底辺がORで同じ、高さは平行線の間で変わらないから、2つの三角形の面積は等しくなる。どう?」
👧 あかり:「完璧だよ。この方法の名前は?」
👦 ゆうと:「待っていました。“等積変形”です。」
合体!△TOR+△SOR → △TSR
👧 あかり:「最後に、△TORと△SORをくっつけると、1つの大きな三角形△TSRになるんだ。」
👦 ゆうと:「あっ、ほんとだ!
左と右の2つがくっついて、ひとつの三角形になった!」
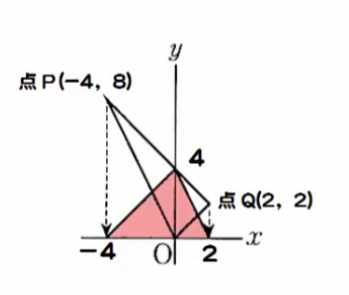
👧 あかり:「Tの x 座標は -4、S の x 座標は 2 だから、TS の長さは \( 2 – (-4) = 6 \)。
底辺 TS = 6、高さ OR = 4。
だから面積は \( \frac{1}{2} \times 6 \times 4 = 12 \) になるね。」
👦 ゆうと:「結果はさっきと同じ12!
でも今度は1回の計算で出せた!」
🌟 あかりのまとめ
👧 あかり:「“等積変形”っていうのはね、
底辺を固定したまま、もう1つの頂点を底辺に平行な線の上で動かしてできた三角形の面積は変わらないという性質のことなんだ。
つまり、底辺を動かさず、もう1つの点を“底辺に平行な線上”で動かせば、
三角形の高さも底辺も同じだから、面積はそのままになるんだよ。
この考え方を使えば、三角形を見やすい形に変えて、
計算を一気に楽にできるんだ!」
👦 ゆうと:「なるほど!
形を変えても、底辺と高さが同じなら面積は変わらないんだね。
まさに“動かして考える数学”だ!」
🎯 放物線×図形の考え方Q&A(ゆうと&あかりの会話)
- Q1. 放物線と直線が出てきたとき、最初に考えることは?
-
👦 ゆうと:「放物線と直線が出てくると、“どこから手をつけたらいいか”わからなくなるんだよね。」
👧 あかり:「最初に考えるのは、“どんな高さで交わるか”=yが同じときを見つけること!
つまり、2つの式を連立してyをそろえるんだよ。
見た目に惑わされず、“同じ高さの場所を探す”って考えると、スッキリするよ。」💡 ポイント: 交点は“yが同じ高さのときのx”を見つけること!
- Q2. どうしてグラフを描いたほうがいいの?
-
👦 ゆうと:「正直、グラフを描くのって面倒…。式だけでやっちゃダメなの?」
👧 あかり:「グラフは“描くこと”が目的じゃなくて、“考えるための道具”なんだ。
線を描くと、どこが高い・低い、どこで交わるがパッと見えるでしょ?
頭の中のモヤモヤを“見える形”にしてくれるのがグラフなんだよ。」💡 ポイント: グラフは「考えを整理するために描く」もの!
- Q3. 図形問題で混乱しないコツは?
-
👦 ゆうと:「点がいっぱい出てくると、何がどの点なのかこんがらがっちゃう…。」
👧 あかり:「そういうときは、“動かないもの”から整理するといいよ。
例えば、y軸・x軸・原点Oみたいに、絶対に動かない場所を最初に押さえる。
そこから“動く点(PやQ)”を考えると、関係がわかりやすくなるよ。」💡 ポイント: まず「動かない基準(軸・原点)」を決めて考える!
- Q4. 面積を出すとき、どこを底辺にすればいいの?
-
👦 ゆうと:「三角形の底辺って、どこを選べばいいのか迷うんだよね。」
👧 あかり:「どこでもいいけど、計算しやすい線を選ぶのがコツ!
たとえば、y軸とかx軸、または座標がわかってる線を底辺にすれば、
高さを“xの距離”や“yの距離”で表せるからスムーズなんだよ。」💡 ポイント: 底辺は“数字で表しやすい線”を選ぶ!
- Q5. 難しい図形の問題を見たとき、どう考え始めればいいの?
-
👦 ゆうと:「問題を見た瞬間、うわっ、ムリ!って思っちゃうんだよね…。」
👧 あかり:「気持ちはわかる!でもね、最初から全部見ようとしないこと。
“わかるところ”だけをまず整理して、数字や文字で表してみるの。
どんなに複雑でも、結局は“数の関係”に直せるから。
見た目よりも、“中身はただの数字のつながり”なんだよ。」💡 ポイント: わかる部分を“数で整理”することからスタート!
🧑🏫 先生からここだけは押さえろ!
🎯 ① 放物線と直線の交点は、「高さ=同じ」のとき!
放物線と直線がぶつかる場所は、2つの式でyが同じとき。
だから、「連立してyをそろえる」=交点を探す、という意味になる。
👉 見た目より「高さの一致」をイメージすること!
🎯 ② グラフは“描くため”じゃなく、“考えるため”に使う!
ノートが汚れてもOK。グラフは頭の中を整理する道具。
描くことで、どこが高い・どこで交わる・対称な位置が目で見える。
👉 「描く=理解を深める動作」として使おう!
🎯 ③ 図形は“動かないもの”から考える!
点が多くて混乱するときは、まずy軸・x軸・原点Oなど
「動かない基準」を先に決めよう。
👉 動かない軸を決めるだけで、図形の関係が一気に整理できる!
🎯 ④ 面積を出すときは、計算しやすい底辺を選べ!
どの線を底辺にしてもOK。だたし、底辺と高さは90°に交わるは忘れない。
コツは「数字で表しやすい線」。
y軸やx軸を使えば、座標から高さをすぐ出せる。
👉 「底辺=計算しやすい線」を選ぶのがプロのやり方!
🎯 ⑤ 等積変形は、“底辺を動かさずに、点を平行に動かす”!
底辺を固定して、もう1つの点を底辺に平行な線の上で動かすと、
三角形の面積は変わらない。
👉 「動かしても、底辺と高さが同じなら面積は同じ!」と覚えよう。
「放物線×図形の問題は、“数字の世界で考える練習”。
グラフを描く → 関係を整理する → 数で考える。
この流れを体で覚えれば、どんな問題でも迷わなくなる!」
🧮 確認問題で定着しよう!(放物線×図形)
✅ 問題①:交点を求める
放物線 \( y = \frac{1}{2}x^2 \) と 直線 \( y = x \)
この2つの交点の座標を求めなさい。
考え方
交点は「同じ高さ(y)で交わる」→ 2つの式を連立して y をそろえる。
\( \frac{1}{2}x^2 = x \)
両辺に 2 をかけて整理すると、
\( x^2 – 2x = 0 \) → \( x(x – 2) = 0 \)
したがって、\( x = 0 \) と \( x = 2 \)。
それぞれを直線の式に代入すると、
\( y = 0 \)、\( y = 2 \)。
✅ 解答: P(0, 0)、Q(2, 2)
✅ 問題②:△POQ の面積
放物線 \( y = -\tfrac{1}{2}x^2 \) と 直線 \( y = x – 4 \) で、
放物線と直線の交点を \( P, Q \) とし、原点を \( O \) とする。
\( \triangle POQ \) の面積を求めなさい。
💡 考え方
放物線 \( y = -\frac{1}{2}x^2 \) と直線 \( y = x – 4 \)。
同じ y のときに交わるから、まず連立して
\( -\frac{1}{2}x^2 = x – 4 \)
両辺に \(-2\) を掛けて整理すると、
\( x^2 + 2x – 8 = 0 \)
\( (x + 4)(x – 2) = 0 \Rightarrow x = -4,\; 2 \)
これを直線の式に代入すると、
\( x = -4 \Rightarrow y = -4 – 4 = -8 \) なので \( P(-4, -8) \)
\( x = 2 \Rightarrow y = 2 – 4 = -2 \) なので \( Q(2, -2) \)
放物線は下に開いている。面積は y 軸で左右に分けて計算する。
直線の y 切片は \( R(0, -4) \) なので、\( OR \) の長さは \( 4 \)。
左(\( \triangle POR \)):底辺 \( OR = 4 \)、高さは点Pのx座標(長さだから+にする) \( = 4 \)。
\( \text{面積} = \frac{1}{2} \times 4 \times 4 = 8 \)
右(\( \triangle QOR \)):底辺 \( OR = 4 \)、高さは点Qのx座標 \( = 2 \)。
\( \text{面積} = \frac{1}{2} \times 4 \times 2 = 4 \)
よって、\( \triangle POQ \) の面積は \( 8 + 4 = 12 \)。
✅ 問題③:
放物線:\( y = \tfrac{1}{2}x^2 \) 直線:\( y = -x + 4 \)
放物線と直線の交点を \( P, Q \) とし、\( O(0,0) \) を原点とする。
\( \triangle POQ \) の面積を求めなさい。
💡 考え方
① まずは交点を求める。\( \frac{1}{2}x^2 = -x + 4 \)
両辺に 2 をかけて整理する。
\( x^2 + 2x – 8 = 0 \Rightarrow (x + 4)(x – 2) = 0 \)
したがって、\( x = -4 \) と \( x = 2 \)。
それぞれを直線の式に代入して、
\( -(-4) + 4 = 8 \) → 点 P(-4, 8)
\( -(2) + 4 = 2 \) → 点 Q(2, 2)
② 直線が y 軸と交わる点は R(0, 4)。
③ 等積変形を使う!
P を通る y 軸に平行な線を引く → x 軸と交わる点を T(-4, 0)
Q を通る y 軸に平行な線を引く → x 軸と交わる点を S(2, 0)
三角形 △POR と △QOR を、それぞれ △TOR と △SOR に “等積変形” すると、
両方合わせて大きな三角形 △TSR になる。
✅ 解答
TS の長さ =2-(-4)= 6、高さ OR = 4
面積 \( = \frac{1}{2} \times 6 \times 4 = 12 \)
👉 △POQ の面積は 12。
🌸「ゆっくりでも、確実に前へ」
👧 あかり:「最近、少しずつわかるようになってきたね。」
👦 ゆうと:「うん。でも、まだむずかしいところもあるよ。」
👧 あかり:「それでいいんだよ。むずかしいって感じるのは、“成長してる途中”ってことだから。」
👦 ゆうと:「途中……?」
👧 あかり:「うん。止まらずに考え続けてる人だけが、最後に“できるようになった”って言えるんだ。
時間がかかっても、悩んでも、投げ出さなかった分だけ力になるよ。」
🌱 ひとこと
どんなに小さな前進でも、それは確実な一歩。
今日できなかったことが、明日できるようになる。
その瞬間のために、君は今、努力してる。焦らなくていい。君の歩幅で、確実に前へ。










