🌟ストーリー解説:相似の“連鎖”を見抜け!
👦ゆうと:「この問題、線がいっぱいあってややこしいなぁ…。どれが相似なのか、全然見えないよ。」
👧あかり:「確かにちょっと複雑だよね。でも、こういう図を見るときのコツがあるんだ。
それは――“平行線が出てきたら、相似を探せ!” ってこと!」
👦ゆうと:「え?平行線が出てきたら相似?どうして?」
👧あかり:「いい質問!
平行線があると、“同位角”や“錯角”が等しくなるでしょ?
そうすると、二つの角が等しい三角形=相似な三角形ができるの。
だから、平行線を見つけた瞬間、“ここに相似がある!”って考えるのがコツなんだよ。」
👦ゆうと:「なるほど。平行線が“相似を見つけるサイン”なんだね。」
👧あかり:「その通り!
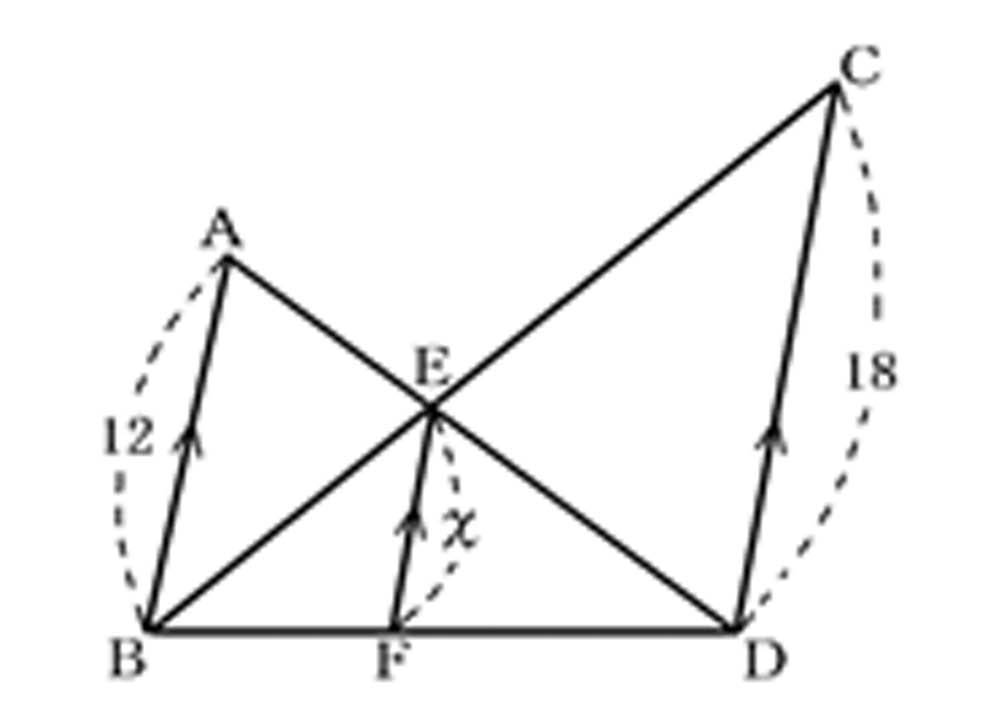
たとえば、この図だと、まず△EABと△EDCを見てみよう。
ABとCDが平行だから、錯角が等しくなって、
∠EAB=∠EDC、∠EBA=∠ECD だから、△EAB∽△EDC が成り立つんだ。
このときの相似比は 12:18=2:3。だから、BE:CE=2:3 になるね。」
👦ゆうと:「ふむふむ。△EAB∽△EDCから2:3が出てきたんだね。」
👧あかり:「そう。そして、ここからもう一つの相似を見つけるんだ。
今度は、△BEFと△BCDに注目してみよう。
ここもEFとCDが平行でしょ?
平行線があるから、同位角が等しく、
∠BEF=∠BCD、∠BFE=∠BDC 。
だから、この2つの三角形も“二角がそれぞれ等しい”から相似になるんだよ。」
👦ゆうと:「あっ、なるほど! 平行線のおかげで、また相似が出てくるんだ。」
👧あかり:「そうなの!
つまり、次の相似を生み出すカギも、やっぱり平行線なんだ。
△BEF∽△BCD だから、今度は BE:BC=2:2+3=2:5 という比が使えるの。
(ここで“2+3”になるのは、BC全体がBEとCEを合わせた長さだからだよ。)
こうして、最初の相似で出した比を次の相似に“つなげていく”ことで、
最終的に EF:CD=2:5=x:18 で、x=7.2と求められるんだよ。」
👦ゆうと:「なるほど!
最初の相似でできた比(2:3)を使って、次の相似(2:5)に進めるんだね。
そして、その流れを作っているのが平行線なんだ!」
👧あかり:「そう! これが“相似の連鎖”の考え方。
一つ見つけた相似を次の相似へつなげていく。
そのつながりを作ってくれるのが、いつも平行線なんだよ!」
🎯先生から ここだけは絶対押さえろ!
🧑🏫「この回のポイントは“平行線が相似を生み出す”ってことだ!
平行線が出てきたら、まず“同位角”や“錯角”が等しくなる。
つまり、二つの角が等しい三角形 ⇒ 相似な三角形ができるんだ。
だからね、平行線を見たら、まず相似を探せ! これは鉄則だよ。
さらにもう一歩。
一つ見つけた相似の中で出てきた“辺の比”は、次の相似にもつながっていく。
これを 『相似の連鎖』 って言うんだ。
最初の相似で出した比を次の相似に引き継いで使うと、
複雑な図形の中でも、答えまで一直線にたどり着ける。
そして、この連鎖をつくるカギを握っているのも、やっぱり平行線。
平行線があるからこそ、次の相似が生まれるんだ。
だから覚えておこう!
👉 平行線を見たら相似を探せ!
👉 相似を見つけたら、その比を次の相似につなげ!
この2ステップができれば、テストで“線がいっぱいの図”が出ても、もう怖くないぞ!」
🔷確認問題
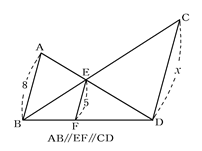
AB // EF // CD のとき、x の長さを求めよ。

👦ゆうと:「この図、また線がいっぱいあるね…。頭がゴチャゴチャしてくる~。」
👧あかり:「平行線が3本あるでしょ? AB // EF // CD。
もうこの時点でチャンス到来!
“平行線があったら、相似を探せ!” だったよね。」
👦ゆうと:「あっ、そうだった! 平行線があると、同位角や錯角が等しくなるんだよね。」
👧あかり:「その通り!
じゃあまず、△AEBと△DCEを見てみよう。
AB // CDだから、∠EAB=∠EDC、∠ABE=∠DCE(平行線の錯角)で、
二つの角がそれぞれ等しいから、△AEB∽△DCE になるね。」
👦ゆうと:「なるほど! じゃあ相似比は、AB:CD=BE:CE=8:x か。」
👧あかり:「その比がポイントなんだよ。
この“8:x”が、次の相似につながっていくんだ。」
👦ゆうと:「次の相似って、どれ?」
👧あかり:「今度は、△BEFと△BCDを見てみよう。
EF // CD だから、また同位角が等しくなって、
二つの角がそれぞれ等しいから、△BEF∽△BCD なんだ。」
👦ゆうと:「なるほど。対応する辺の比は BE:BC になるね。」
👧あかり:「そう。ここで重要なのは、BC は BE+EC だということ。
最初の相似で出した BE:CE=8:x を使うと、
BE:BC=8:(8+x) になるの。」
👦ゆうと:「わかった! じゃあ、△BEF∽△BCD から EF:CD=5:x だから、
比のつなぎ方は 8:(8+x)=5:x だね!」
👧あかり:「そのとおり!
これを解くと、8x=5(8+x)
8x=40+5x
3x=40
x=40/3(cm)になるね。」
👦ゆうと:「できた! さっきの“比のバトンリレー”って、こういうことか!」
👧あかり:「バッチリ!
大事なのは、平行線があるたびに“相似を探す”こと、
そして、“相似比を次の相似へつなぐ”こと。
この問題は、まさに“相似の連鎖”を使う練習問題なんだよ!」
🧩まとめコメント
👧あかり:「平行線が3本あるときは、相似が2つできるのが定番!
まず1つ目の相似で比を出して、次の相似につなげる。
つまり、“比のバトンリレー”=相似の連鎖なんだ。」
👦ゆうと:「なるほど。
平行線を見たら“相似を探す”、相似を見つけたら“比をつなぐ”!
これでテストでも見抜けそうだね!」










