🌟中3数学 相似の見つけ方&決定のコツ|相似決定の図で完全攻略!
👦ゆうと:「ねぇあかり、相似の問題って“対応する辺”を間違えると一気にわからなくなるんだよね。」
👧あかり:「わかる〜! 角が等しいとか、辺の比とかはまだいいけど、
“どの辺とどの辺が対応してるか”って、けっこう迷うよね。」
👦ゆうと:「だって図の向きも違うし、どっちが大きいかもバラバラだし…。」
👧あかり:「そう! でもね、“相似決定の図”が書けるようになると、
対応する辺や角がスッと見つけられるようになるんだよ。
しかも、この図が書けるってことは、もう証明も書けるってこと!
だから、この“相似決定の図”の書き方――つまり使い方をマスターしちゃえば、
相似の問題は一気に楽になるよ!」
👦ゆうと:「なるほど…! 対応の見つけ方がカギなんだね!」
👧あかり:「うん。今日はそのやり方を、マックスメソッドでいっしょに整理してみよう!」
① 二組の角がそれぞれ等しい
手順(図を見ながら同じ順でやってみよう)
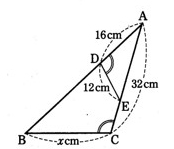
🔹1)大きい方の三角形を描く。
👧あかり:「まず△ABCを写して、わかっている角に印をつけよう。」
🔹2)比較する小さい三角形も、向きをそろえて小さく描く。
👦ゆうと:「向きをそろえるって、どういうこと?」
👧あかり:「大きい△ABCと同じ向きで三角形を描くんだよ。
この時は、まだ小さい三角形の記号は入れちゃだめ。それを決めるために図を描いていることを忘れないで。」
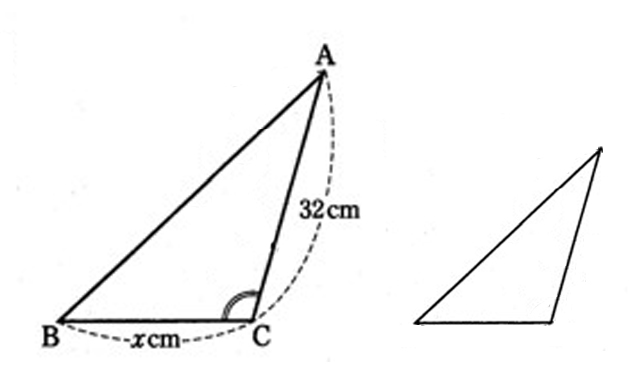
🔹3)共通や仮定の角に印を入れる
👧あかり:「次に、“どの角が等しいのか”を図で確かめよう。
今回の条件は、∠ACB=∠ADE って書いてあるね。
だから、この2つの角に“仮定”の印をつけよう。」
👧あかり:「印をつけると、どの角が対応しているかが一目でわかるよね。
このとき、小さい三角形では右下の角がDだってことも自然に決まるんだよ。」
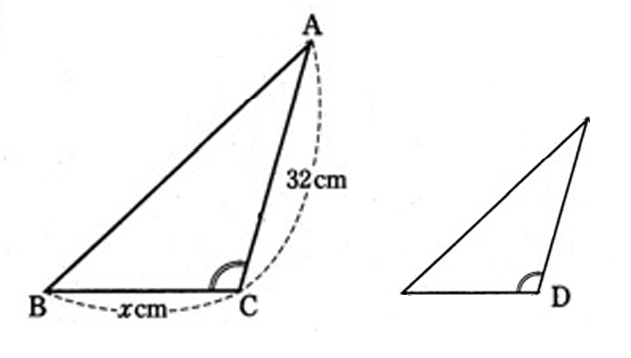
👦ゆうと:「なるほど! 角に印を入れるだけで、対応の位置まで分かるんだね。」
👧あかり:「そう。さらにもう1つ! Aの角は大きい三角形と小さい三角形で共通だから、“共通”の印も入れるよ。
これで、小さい三角形の上の角がAだって決まった。
残った角は自動的にEになるね。」
👧あかり:「こうやって“仮定”と“共通”の印を入れると、
どの角がどこに対応しているかが自然に浮かび上がるんだ。
そして、2つの角がそれぞれ等しいってことが、図を見ただけでハッキリ分かるようになるよ。」
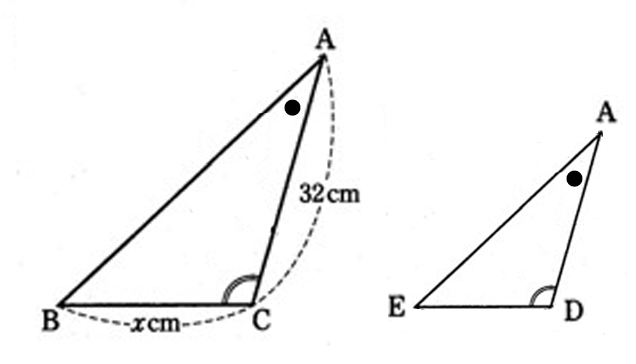
🔹4)これで“相似決定の図”が完成!
👧あかり:「ここまでで、印をつけた角の位置が決まったね。
Aは共通、右下の角がD、残りの角がE。
つまり、小さい△ADEと大きい△ACBでは、
二組の角がそれぞれ等しいことがわかったよ。」
👦ゆうと:「ってことは、これで相似って言えるんだね?」
👧あかり:「そう! 二組の角がそれぞれ等しいから、
△ACB∽△ADE になるんだ。
これが“相似決定の図”のすごいところ!
図を描いて印を入れるだけで、
相似になる理由が目で見て分かるようになるんだよ。」
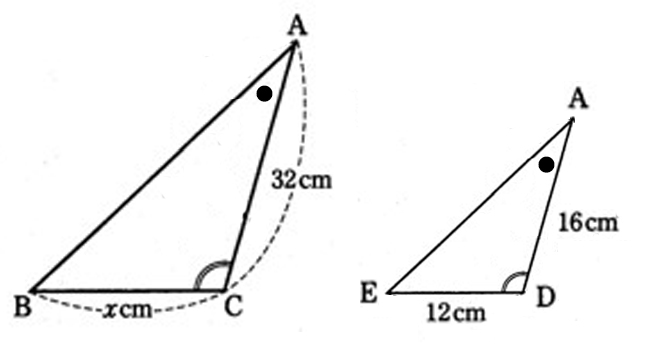
🔹5)対応順で比を書いて、x(BCの長さ)を求めよう!

👧あかり:「相似が分かったら、対応する辺を確認しよう。
大きい三角形のACと小さい三角形のADが対応しているから、
AC:AD=32:16=2:1になるね。」
👦ゆうと:「だから、BC:EDも2:1だから、x:12=2:1ってことか。」
👧あかり:「そう! だから、x=24cm。
相似の比を使えば、長さもスッキリ求められるね!」
🔹6)“相似決定の図”を見ながら証明を書く
👧あかり:「最後に、この“相似決定の図”をもとにして、証明を書いてみよう。
図が描けていれば、証明も自然に書けるんだよ。」

証明
△ACBと△ADE において、
∠ACB=∠ADE(仮定)
∠CAB=∠DAE(共通)
よって、二組の角がそれぞれ等しいので、
△ACB∽△ADE。
👦ゆうと:「なるほど。相似決定の図を描いた順番で、そのまま証明が書けるんだね!」
👧あかり:「そう! “図が描ける=証明が書ける” っていうのは、こういうことなんだよ。」
💡まとめコメント
👧あかり:「相似決定の図をマスターすれば、角の対応・辺の比・相似の理由、そして証明まで、
すべて“ひとつの流れ”で整理できるようになるよ。
これで相似の問題は、もう迷わないね!」
② 二組の辺の比とその間の角がそれぞれ等しい
手順(図を見ながら、同じ順でやってみよう)
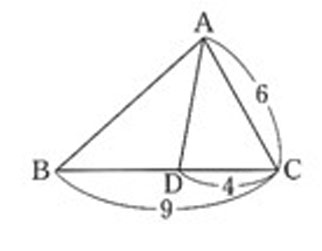
🔹1)大きい方の三角形を描く
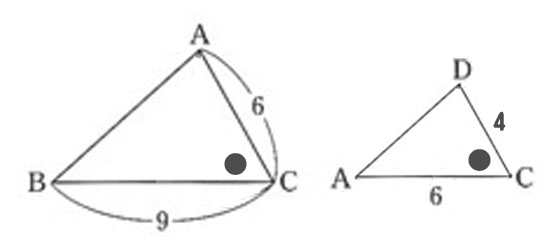
👧あかり:「まず△ABCを描いて、わかっている長さと角の情報を入れよう。
ここでは、辺BC=9cm、AC=6cm、∠Aがわかっているね。」
👦ゆうと:「OK! じゃあ次は小さい方の三角形を描けばいいんだね。」
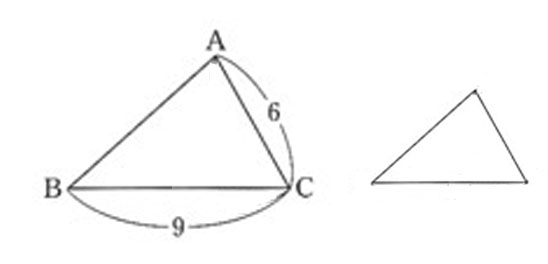
🔹2)比較する小さい三角形も、向きをそろえて描く
👧あかり:「そうそう。大きい△ABCと同じ向きで小さい△ADEを描こう。
向きをそろえると、対応が分かりやすくなるよ。
まだ記号(AやEなど)は入れずに、位置関係を見ながら形を決めるのがポイント!」
👦ゆうと:「なるほど。まず形を合わせて、それから頂点を決めていくんだね。」
🔹3)共通や仮定の角に印を入れる
👧あかり:「次に、“どの角が等しいのか”を確かめよう。
今回の条件は“その間の角が等しい”だから、∠Cが共通だね。
ここに“共通”の印を入れておこう。」
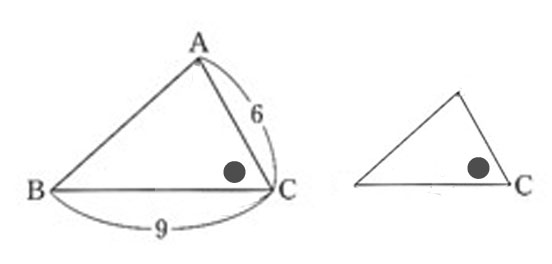
👦ゆうと:「共通の角があるから、そこをはさんだ2本の辺を比べるんだね。」
👧あかり:「そのとおり! 角Cから出ている2本の辺に注目するよ。」
🔹4)辺の比を確かめる
👧あかり:「角Cから出る2本の線に注目してみよう。
大きい三角形△ABCでは、角Cから出ているのはCBとCA。
CBのほうが長いね。」
👦ゆうと:「うん、BCのほうが長くて、CAはちょっと短いね。」
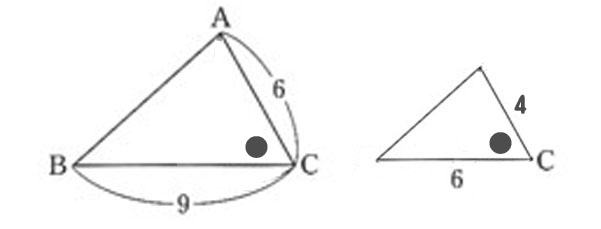
👧あかり:「小さい三角形でも、角Cから出ているのはCAとCD。
同じように、CAのほうが長いね。
だから、大きい三角形で“長い方の辺”に対応するのは、小さい三角形でも“長い方の辺”。
つまり、大きい三角形のBの位置に、小さい三角形ではAが対応することがわかるんだ。」
👦ゆうと:「なるほど。長いほうの辺どうしを対応させれば、頂点の位置も自然に決まるんだね!」
👧あかり:「そう。これで、対応する角と辺の位置が決まったから、あとは比を確かめよう。」
👧あかり:「長辺どうしは BC:AC=9:6=3:2。
短辺どうしは AC:DC=6:4=3:2。
2辺の比が3:2でそろっているね!」
👦ゆうと:「ってことは、“二組の辺の比が等しい”ってことになるね。
しかも、その間の角Cで共通だから、相似が言えそう!」
👧あかり:「その通り! 二組の辺の比とその間の角がそれぞれ等しいとき、
2つの三角形は相似になるんだよ。」
🔹5)これで“相似決定の図”が完成!
👧あかり:「ここまでで、“相似決定の図”ができたね。
角Cが共通で、そこから出る2本の辺の比が等しいから、
△ABC∽△DAC と言えるんだよ。」

👦ゆうと:「ほんとだ! 図を描いて印を入れるだけで、相似の理由が目で見てわかるね。」
🔹6)“相似決定の図”を見ながら証明を書く
👧あかり:「最後に、この“相似決定の図”をもとにして、証明を書いてみよう。
図が描けていれば、証明も自然に書けるよ。」

証明
△ABC と △DAC において、
∠ACB=∠DCA(共通) … ①
BC:AC=9:6=3:2 … ②
AC:DC=6:4=3:2 … ③
①、②、③より、
二組の辺の比とその間の角がそれぞれ等しいので、
△ABC∽△DAC
👦ゆうと:「なるほど。角を共通にして、その角から出る2本の辺の比が同じなら、相似って言えるんだね。」
👧あかり:「そう! “角の位置を合わせて、その角から出る2本の辺を比べる”ことがポイントだよ。
これがわかると、相似の問題は一気に楽になるよ!」
💡まとめコメント
👧あかり:「どちらの型でも大事なのは、“向きをそろえて描くこと”!
向きをそろえると、角や辺の対応が自然に見えてくるんだ。」
👦ゆうと:「対応がはっきりすれば、比もスッキリ整理できるね。
印をつけて“相似決定の図”を描くと、2つの三角形の形が同じ理由が目で見てわかる!」
👧あかり:「そう! 図を描いて対応を“見える化”すれば、
相似の証明もスラスラ書けるようになるよ。」
🎯先生から:ここだけは絶対に押さえろ!
① “相似決定の図”を描ける=相似が理解できている!
図を描くことで、「どの角が対応しているのか」「どの辺を比べるのか」が一目でわかるようになる。
描けるようになるということは、もう証明の流れを自分でつかめているということ!
② “向きをそろえる”ことを忘れない!
大きい三角形と小さい三角形を同じ向きで描くと、対応の順番や角の位置が自然に決まる。
これができると、後のミスがぐっと減るぞ!
③ “印をつける”=“対応を決める”と思え!
仮定や共通の角に印を入れるたびに、頂点の位置関係が自動的に見えてくる。
印は「見える証拠」だから、ためらわずに入れていこう!
④ “相似決定の図”を書く力が、証明力につながる!
ただ図を写すだけじゃなく、自分の力で「相似決定の図」を描けるようになることが本当のゴール。
描きながら、何が共通で、どの辺が対応しているのかを“整理する技術”を身につけよう。
この図が描ければ、証明も自然に書けるようになる!
⑤ “図が描ける=証明が書ける”
相似決定の図を描くと、証明の流れそのものが見えてくる。
順番通りに印をつけて、理由を書くだけでOK。
難しいと感じたら、まず図を描くことから始めよう!
💬ひとことアドバイス:
👨🏫先生:「“相似決定の図”は、相似の問題を解く“地図”みたいなもの。
図を描いて対応を整理してみよう。
正しく描けた瞬間に、もう答えは見えてるぞ!」
🎯相似の証明 確認問題
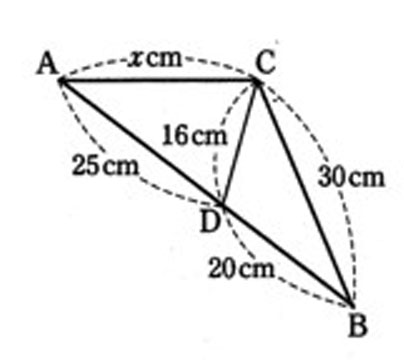
【問題1】
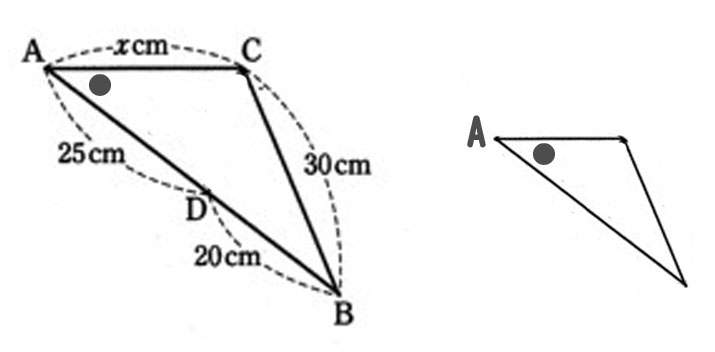
相似決定の図を描いて、証明して、ACの長さを求めよ。

△ABCをサッと写して、長さや角度の情報を入れておこう。

小さい三角形を書く。△ACDを考える。 角Aは共通。
小さい三角形で角Aから出る辺は25cmとxcm。どちらが長いか決められない。
⇒ △ACDではうまくいかない。 失敗。 別な三角形で考えよう。△CDBにして見よう。
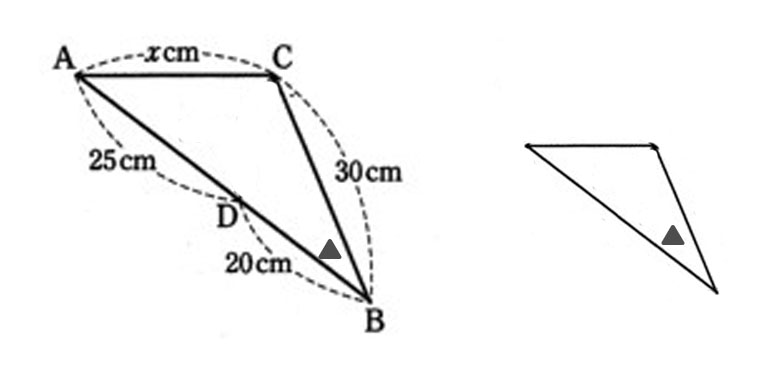
角Bが共通。
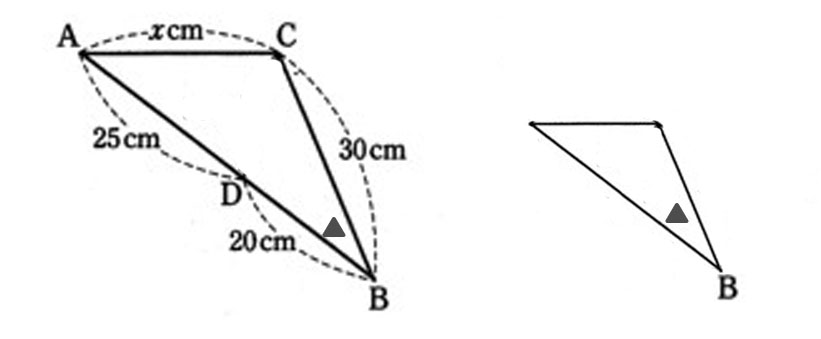
小さい三角形で角Bから出る辺は20cmと30cm。今度は決められる。
角Bから30cm先は角C、角Bから20cm先は角D。
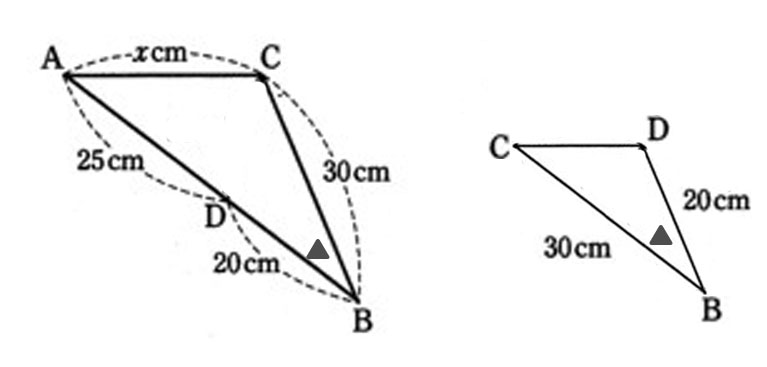
対応する辺はAB:CB=45:30=3:2
CB:DB=30:20=3:2で、二組の辺の比とその間の角がそれぞれ等しいから、
△ABC∽△CBD
AC:CDも3:2だから、x:16=3:2
x=24cm AC=24cm
証明
△ABC と △CBD において,
∠ABC=∠CBD(共通) …①
AB:CB=45:30=3:2 …②
CB:DB=30:20=3:2 …③
①,②,③より,二組の辺の比とその間の角がそれぞれ等しいから,
△ABC∽△CBD
また,相似比は AB:CB=AC:CD=3:2 より,
AC:CD=3:2
AC:16=3:2 だから AC=24cm
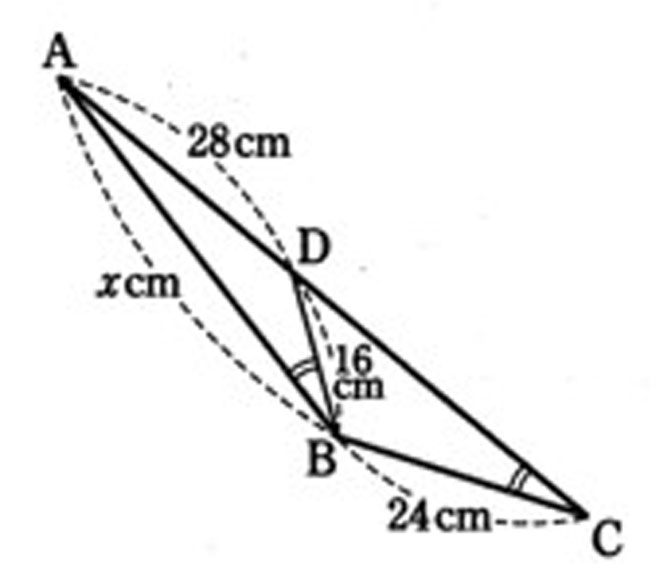
【問題2】
相似決定の図を描いて、証明して、ABの長さを求めよ。

1)大きい三角形を写す(△ABC)
2)小さい三角形を、向きをそろえて写す
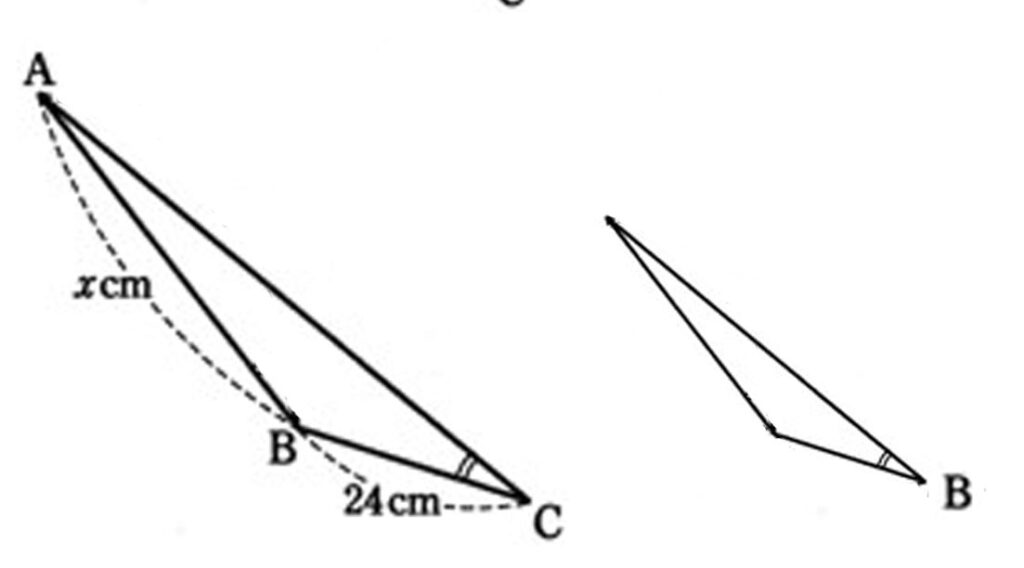
仮定から∠ACBと∠ABD(∠DBA)が同じ大きさ。
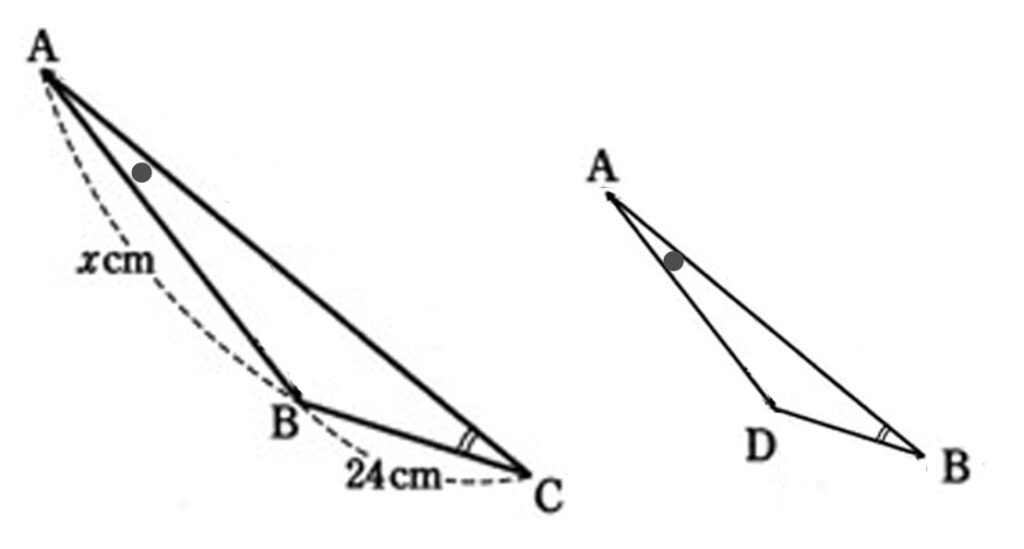
∠Aは共通。
これで、2角がそれぞれ等しいから、△ABC∽△ADB
3)相似比を求めて、ABの長さを出す。
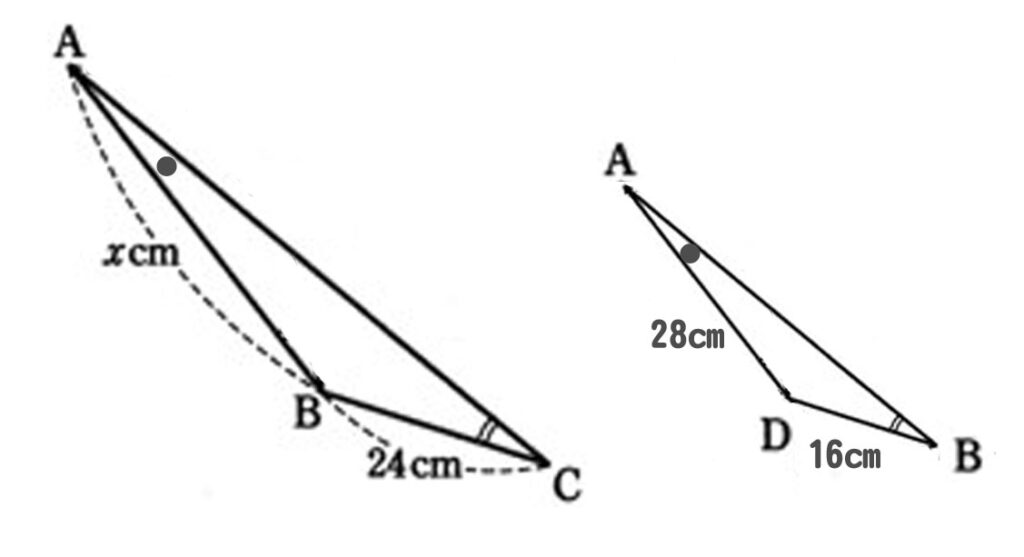
相似比は、BC:DB=24:16=3:2
よって、AB:28=3:2
AB(x)=42cm
4)証明
△ABCと△ADBで、
∠ACB=∠ABD (仮定) …①
∠BCA=∠DAB (共通) …②
①、②より2角がそれぞれ等しいから、
△ABC∽△ADB
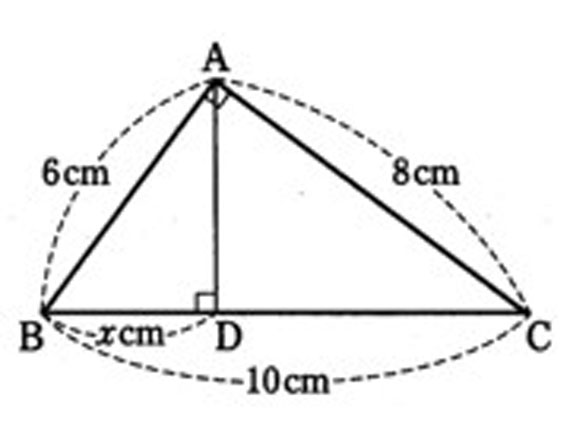
【問題3】
相似決定の図を描いて、証明して、BDの長さを求めよ。

1)大きい三角形を写す(△ABC)
2)小さい三角形を、向きをそろえて写す
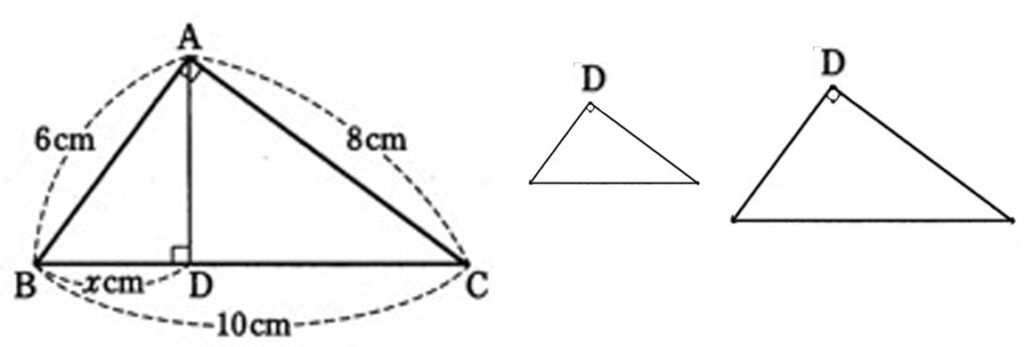
90°が3個所にあるので、△ABCと相似になる候補は2つある。
△ABCを小さくして、2つの三角形を描く。
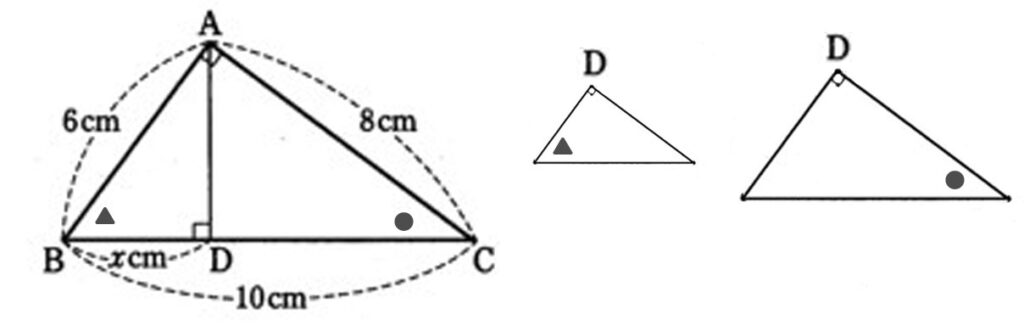
小型の三角形は、左下の角が元の三角形の∠Bと共通で、∠Bとなり、
2角がそれぞれ等しいから相似。
中型の三角形は、右下の角が元の三角形の∠Cと共通で、∠Cとなり、
2角がそれぞれ等しいから相似。
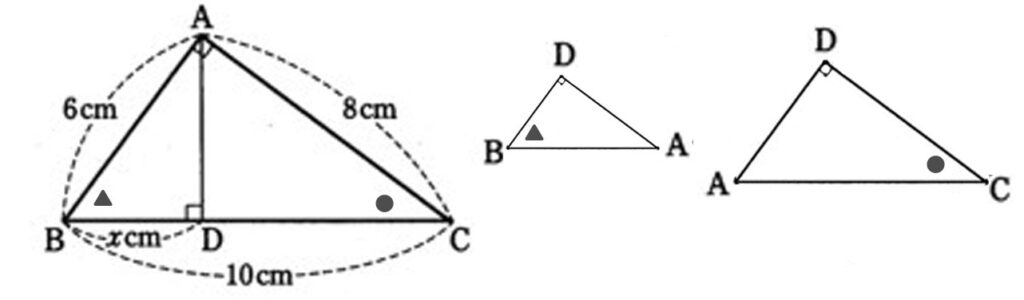
△ABC∽△DBA (2角がそれぞれ等しい)
△ABC∽△DAC (2角がそれぞれ等しい)
3)相似比を求めて、ABの長さを出す。
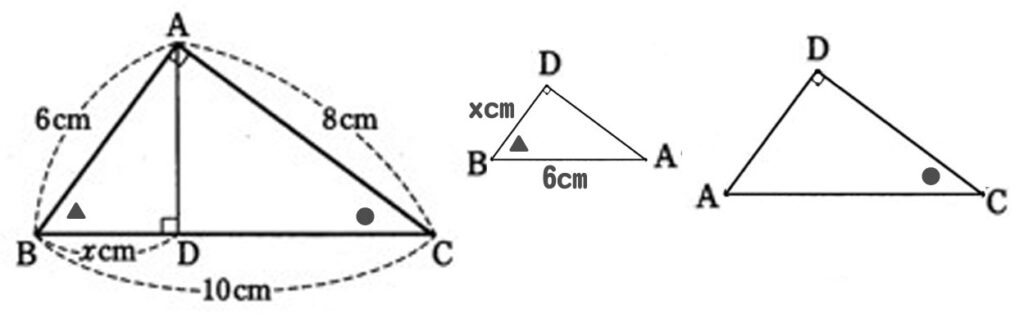
△ABC∽△DBAの相似比はBC:BA=10:6=5:3
よって、6:DB=5:3 DB(x)=3.6cm
4)証明
△ABCと△DBAで、
∠BAC=∠BDA=90° (仮定) …①
∠ABD=∠DBA (共通) …②
①、②より2角がそれぞれ等しいから、
△ABC∽△DBA