こんにちは！みんなはテストの点数を見たときに「自分はクラスの中でどのあたりの位置？」とか「1番の人とどれくらい差があるんだろう？」と思ったことはないかな？ そんなときに役立つのが「四分位数」なんだ！今回は、データの分布を詳しく知るために四分位数を活用する方法と、そのデータを視覚的に表す「箱ひげ図」の書き方を解説するよ！
四分位数ってなに？
四分位数という名前を聞くと、「なんだかすごく難しそう…」と思うかもしれませんが、実はとてもシンプル！
例えば、マラソン大会に出場したとします。全員のタイムを速い順に並べたときに、「このタイムなら上位25%に入る」「ここがちょうど真ん中」「このタイムであれば下位25%以内」といった情報を知りたいときに使うのが四分位数です。
データの分布を4つの部分に分ける区切りの値（数字）のことを「四分位数」といいます。
まずは、四分位数を理解するために、データの真ん中を示す「中央値」（中1数学）から復習してみましょう。
中央値を求めよう！
例えば、16人の数学のテストの点数が次のようだったとします。
33, 87, 45, 68, 86, 92, 72, 73, 96, 73, 15, 28, 56, 71, 88, 73
これを小さい順に並べると、
15, 28, 33, 45, 56, 68, 71, 72, 73, 73, 73, 86, 87, 88, 92, 96
データの個数が奇数の場合は、真ん中の1つの値が中央値になります。しかし、データが偶数個（16個）の場合、真ん中に2つの値があるため、その平均を求める必要があります。8番目と9番目の値（72点と73点）の平均をとると、
(72 + 73) ÷ 2 = 72.5
よって、中央値は72.5点となります。
四分位数を求めよう！
四分位数はデータを4つのグループに分ける区切りの値です。
- 第1四分位数（Q1）：データの下位25%の境目
- 第2四分位数（Q2）：中央値（データの50%の境目）
- 第3四分位数（Q3）：データの上位25%の境目
さっそく求めてみましょう！
1. 第1四分位数（Q1）
中央値より小さいデータ（前半の8個）：
15, 28, 33, 45, 56, 68, 71, 72
この中央値（4番目と5番目の平均）を求めると、
(45 + 56) ÷ 2 = 50.5
第1四分位数は50.5点
2. 第3四分位数（Q3）
中央値より大きいデータ（後半の8個）：
73, 73, 73, 86, 87, 88, 92, 96
この中央値（4番目と5番目の平均）を求めると、
(86 + 87) ÷ 2 = 86.5
第3四分位数は86.5点
四分位数のまとめ
| 四分位数 | 値 |
|---|---|
| 第1四分位数（Q1） | 50.5点 |
| 第2四分位数（Q2） | 72.5点（中央値） |
| 第3四分位数（Q3） | 86.5点 |
箱ひげ図を描いてみよう！
四分位数が分かると、データの分布を「箱ひげ図」というグラフで表すことができます。
箱ひげ図の作成手順
- データの5つの要素を求める
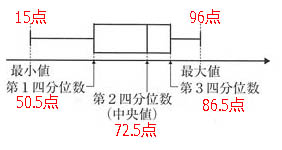
- 最小値：15点
- 第1四分位数（Q1）：50.5点
- 第2四分位数（Q2、中央値）：72.5点
- 第3四分位数（Q3）：86.5点
- 最大値：96点
- 数直線を描く
- 点数の範囲を示す数直線を用意します。
- 箱を描く
- 第1四分位数（50.5）と第3四分位数（86.5）を結ぶ長方形を描きます。
- これが「箱」となり、データの中間50%がどこに分布しているかを示します。
- ひげを描く
- 箱の両端（Q1とQ3）から最小値（15）と最大値（96）までの線を引きます。
- これを「ひげ」と呼びます。
- 中央値を示す
- 箱の中に、第2四分位数（中央値）の位置に縦線を引きます。
動画で復習
まとめ
✅ 四分位数は、データを4つのグループに分ける区切りの値！
✅ 第1四分位数（Q1）、第2四分位数（Q2：中央値）、第3四分位数（Q3）を求めることで、データの散らばりを詳しく分析できる！
✅ 箱ひげ図を描くことで、データの分布を視覚的に捉えやすくなる！
箱ひげ図は、データのばらつきを簡単に視覚化できる便利なツールです。特に、最大値や最小値、中央値、四分位数の位置が一目で分かるのが特徴です。
箱ひげ図を描く具体的な手順
- データを昇順に並べる
- 最小値、最大値、第1四分位数（Q1）、第2四分位数（中央値）、第3四分位数（Q3）を求める
- 数直線を引き、Q1とQ3を結ぶ長方形（箱）を描く
- 箱の中央に中央値の位置を示す縦線を引く
- 箱の両端から最小値・最大値までの線（ひげ）を引く
これで、データのばらつきや中心が視覚的に分かりやすくなります！
四分位数をマスターすれば、データ分析の達人になれるかも！？
次のテストの点数や身の回りのデータを使って、四分位数を求めてみよう！
練習問題
次のデータの四分位数を求めてみよう。
データ：12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48
ヒント：データの並べ替え、中央値の計算、第1・第3四分位数の求め方を思い出してみよう！
😊「なんだ。簡単じゃん」と感じてもらえたらすごくうれしいです。わかりにくい問題があったら、教えてください。簡単に説明したり、わかりやすい他の方法で、もっと楽に理解が深まります。
「ブログより実際に話しがしたい」「もっといろいろ教えてほしい！」と感じた人は、無料体験や相談に来てください！ この先生に相談をすることや習うことができます！ 少し勇気を出して、ぜひ一度体験しに来てください！ 「わかるって面白い」とか成績が良くなる自分を感じられる日がきます。お問い合わせ・ご質問はこちらです。
