小学校5年生で学ぶ「割合」は、算数の中でも特に重要な単元であり、中学・高校の数学でも頻繁に利用されます。しかし、多くの小学生がこの単元でつまずいてしまうのも事実です。
今回は、お子様が「割合」をスムーズに理解し、活用できるようになるための具体的な方法を、保護者の皆様に向けて解説します。
1. 「割合」って一体何？
割合というのは、 「どれくらいの大きさなのか」を表します。
具体例で考えてみましょう！
クッキーが 10枚 あります。そのうち 2枚 を食べました。
このとき、食べたクッキーは全体のどれくらい？
全体のクッキーの枚数（基準になる量）は 10枚。
食べたクッキーの枚数（くらべる量）は 2枚。
「割合」は、 （基準になる量）10枚に対して、（くらべる量） 2枚は、どのぐらいの大きさなのかを表します。
2. 多くの小学生が「割合」でつまずく理由
- 抽象的な概念：「もとにする量」「くらべられる量」「割合」の関係を理解するのが難しい。
- 複数の計算方法：問題によって、かけ算、割り算を使い分ける必要がある。
- 文章題への苦手意識：文章から必要な情報を読み取るのが苦手。
3. 家庭での教え方：４つのステップ
ステップ１：視覚的に理解する
まずは、具体的なものを使って割合を視覚的に理解させましょう。
- 例1：10cmのテープを基準にして、5cmのテープは何倍ですか？
- 5cmのテープを10cmのテープに重ねると、半分ですね。つまり、0.5倍です。
- 例2：クッキーが10枚あります。そのうち2枚食べました。食べたクッキーは全体の何％ですか？
- 全体の10枚を10個のブロックで表し、食べた2枚を別の色のブロック2個で表します。全体の10個に対して2個なので、2/10 = 0.2 です。
ステップ２：「もとにする量」「くらべられる量」「割合」を明確にする
問題文から、「もとにする量」「くらべられる量」「割合」をそれぞれ何かを明確にすることが重要です。
「く」＝くらべられる量 「も」＝もとにする量 「わ」＝割合 の図を書いて整理すると分かりやすくなります。
- く：くらべられる量 (例：5cm、食べたクッキー2枚)
- も：もとにする量 (例：10cmのテープ、クッキー全体10枚)
- わ：割合 (例：0.5倍)
問題文をよく読んで、どの量がどれに当たるかを正しく見つける練習をしましょう。
初歩の段階では、手掛かりとして次に手順と方法を活用してください。
① 最初に「わ」（割合）を見つけます。
見つけ方は、問題文の中で「～倍」「～％」「～割」などが割合です。
② 次に「も」（もとにする量）を見つけます。
見つけ方は、問題文で割合の前にある「～の」の前にある数。
③残った数が、「く」（くらべられる量）です。
ステップ３：計算方法は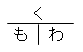 
を使う
3-1. 基本ルール：「く」「も」「わ」の関係
「く」「も」「わ」の関係は、以下のように表されます：
- 横棒（÷）：割り算を表します。
- 縦棒（×）：かけ算を表します。
このルールを使えば、どの項目がわからなくても、他の2つを使って計算できます。
3-2. 「く」（くらべられる量）がわからない場合
- 「も」（もとにする量） と 「わ」（割合） がわかっています。
- 「く」と「も」「わ」の間は 縦棒（×） なので、以下のように計算します： く=も×わ
例題：
問題：「100cmの30%は何cmですか？」
- 「わ」（割合） = 30% = 0.3
- 「も」（もとにする量） = 100cm
- 「く」何cm
計算：く=も×わ=100×0.3=30
答え：30cm
3-3. 「も」（もとにする量）がわからない場合
- 「く」（くらべられる量） と 「わ」（割合） がわかっています。
- 「く」と「わ」の間は 横棒（÷） なので、以下のように計算します： も = く ÷ わ
例題：
問題：「40cmは全体の20%です。全体の長さは何cmですか？」
- 「わ」（割合） = 20% = 0.2
- 「も」全体の長さ
- 「く」（くらべられる量） = 40cm
計算：も=く÷わ=40÷0.2=200
答え：200cm
3-4. 「わ」（割合）がわからない場合
- 「も」（もとにする量） と「く」（くらべられる量） がわかっています。
- 「く」と「も」の間は 横棒（÷） なので、以下のように計算します： わ=く÷も
例題：
問題：「50cmは200cmの何%ですか？」
- 「わ」何％
- 「も」（もとにする量） = 200cm
- 「く」（くらべられる量） = 50cm
計算：わ=く÷も=50÷200=0.25 0.25 = 25%
答え：25%
3-5. まとめ：「く」「も」「わ」の活用方法
| わかっているもの | 計算式 | 使用する棒 |
|---|---|---|
| 「く」がわからない | く=も×わ | 縦棒（×） |
| 「も」がわからない | も=く÷わ | 横棒（÷） |
| 「わ」がわからない | わ=く÷も | 横棒（÷） |
3-6. 家庭での練習ポイント
- 問題文を読んで「く」「も」「わ」を整理する
「どの量がどれに当たるか」を明確にし、ノートに書き出しましょう。 - 計算式をノートに書いて練習する
式と答えを丁寧に書き出すことで、問題の理解が深まります。
この単元は、算数の中でも特に理解に時間がかかるものです。お子さまがつまずかないようにするために、しっかりとした時間配分と効果的な教え方が必要です。
割合の指導に時間をかける理由
「割合」は、初めて学ぶ際には、新しい概念と計算方法を同時に理解しなければならない難しい単元です。この段階で十分な理解が得られないと、中学・高校での「比」や「割合を用いた応用問題」でさらに苦労してしまうことがあります。
そこで、多めの時間を確保してじっくり取り組むことが重要です。焦らずに進めることで、お子さまが「割合」の仕組みをしっかりと理解し、使いこなせるようになります。
初めての割合指導は「く」「も」「わ」の確認から
私自身、これまでさまざまな方法を試してきましたが、初めて割合を学ぶ5年生には、まず以下のように進めるのが効果的だと感じています。
1. 「く」「も」「わ」の確認を徹底する
- 「く」：くらべられる量
例：何を求めたいのか？（例：ある商品の割引額、何本の鉛筆が必要か） - 「も」：もとにする量
例：基準となる値はどれか？（例：商品の元の価格、全体の人数） - 「わ」：割合
例：何倍、何割、何％といった基準に対する比率。
2. 一つ一つの要素を明確にする
問題文を読み、どの数字が「く」「も」「わ」に該当するかをノートに書き出します。これを徹底することで、問題の理解が深まります。
計算方法は公式を活用するのが現実的
「割合」を求める計算は、以下の3つの公式で解けます：
- 割合を求める わ = く ÷ も
- くらべられる量を求める く = も × わ
- もとにする量を求める も=く÷わ
ただし、これらを使いこなすのは簡単ではありません。特に慣れていないうちは、「かけるのか」「わるのか」が混乱してしまう子が多いです。 また、しばらくたつと、「あれ？ かけるんだっけ？ わるんだっけ？」となる子がすごくたくさんいます。
「く」「も」「わ」を活用した教え方のメリット
公式に頼りすぎると混乱してしまうお子さまにとって、を使った方法は効果的です。具体的には：
- 問題文を読む → 「く」「も」「わ」を書き出す
- 公式ではなく「く」「も」「わ」の位置関係をイメージ
- 横棒（÷） は割り算を表す。
- 縦棒（×） はかけ算を表す。
これを繰り返すことで、公式に頼らなくても自然に計算方法が身につきます。
子どものノートの例
まとめ
「割合」は、一度しっかり理解すると、今後の算数・数学の基礎となる重要な単元です。特に小学校5年生の段階では、焦らずじっくりと「く」「も」「わ」を確認しながら進めることが成功のカギとなります。
お子さまが混乱しないよう、明確な手順を示しつつ、「割合」の仕組みを楽しく学べるようサポートしていきましょう！
何かご質問がございましたら、どうぞお気軽にご相談ください。
