【小5算数教室】 単位量
【保存版】小5でつまずかない!“対応表”でスッキリわかる「1あたりの数」の教え方
このブログシリーズでは、小学生がつまづきやすい算数の単元をテーマに、ご家庭でも実践できる教え方のコツや、考える力が育つ声かけの工夫をご紹介しています。 どれも、実際に合格屋マックスの算数教室で実践しているものです。家庭で「どう教えたらいいか分からない」と思われる方も、ぜひ参考にしてみてください。
「計算のルールを覚える」だけではなく、「意味を理解して使える力にする」ことが、この時期の算数では特に大切です。
□ 単位量って何?
単位量とは「1つあたり」の量や「1単位あたりの値」を表します。 ばらばらに見える数量を、「1つあたり」に縛って比較したり、全体を求めたりできるので、小学算数の土台になります。
□ 問題! 実際にやってみよう
例題:6個300円の消しゴム、1個の値段は?
【対応表】
| 個数 | 価格 |
|---|---|
| 6個 | 300円 |
| 1個 | ?円 |
この問題を「対応表」にすると、以下のような構造になります:
「対応表」を作るポイントは、“同じ単位の数をタテにそろえることです。
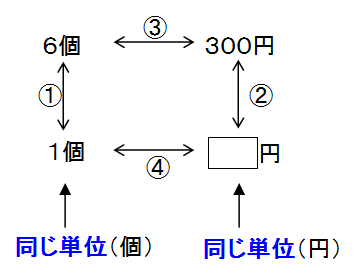
①,②は同じ関係。 ①は下から上に6倍(×6)だから、逆に上から下は÷6
②と①は同じ関係だから、②も下から上に6倍(×6)で、逆に上から下は÷6になる。
だから、300÷6=50円
「対応表」では、左側の上下の関係とも右側の上下の関係が同じになることがポイントです。
□ 人口密度の問題
例題:
- A市は84km^2の面積に235,200人
- B市は57km^2の面積に165,300人
どっちの市が「面積あたり」の人口密度が高い?
【対応表】
| A市 | 面積(㎢) | 人口 |
|---|---|---|
| 84 | 235,200人 | |
| 1 | ?人 |
左側で下から上に×84、上から下に÷84だから、人口密度は、235,200 ÷ 84 = 2,800人
| B市 | 面積(㎢) | 人口 |
|---|---|---|
| 54 | 165,300人 | |
| 1 | ?人 |
左側で下から上に×54、上から下に÷54だから、人口密度は、165,300 ÷ 54 = 2,900人
→ 人口密度が高いのは B市!
このように、対応表の上下関係がはっきりすると、計算の意味も明確になります。
もう意味も考えないで、かけるの? わればいいの? は、終わりにしましょう。
□ 家庭でやってみよう
ポイント:「1あたり」を日常生活で見つける
- 「1個あたりの価格は?」
- 「1gあたりはいくら?」
- 「1時間に何km進む?」
ポイント:対応表を自分で作る
問題の解決はすぐにせず、表にして考えることを習慣にしていきましょう。
ポイント:声かけの工夫
- 「この問題の『1つあたり』は?」
- 「対応表にすると?」
□ 教え方のプロのコツ
対応表は「上に元の情報」「下に求めたい情報」
上の段に「もとになるデータ」、下の段に「知りたいこと」を書き、縦に単位をそろえると、関係が見えやすくなります。
上から下・下から上の「計算の関係」を意識させる
たとえば、上が6個、下が1個なら、「上から下は÷6」「下から上は×6」。この関係は左右どちら側にもそのまま当てはまります。縦の関係が同じ計算でつながることを意識させましょう。
単位の変換に気をつける
gとkg、分と時間など、単位がそろっていないと正しく比較できません。表に書く前に「この単位でいい?」と一声かけて確認するクセをつけましょう。
以下、ちょっと余談です。
最近、小学生の子どもたちと接していて感じるのは、「単位」をあまり意識しないまま計算してしまう子が増えていることです。たとえば、「cm」と「cm²」の違いに気づいていなかったり、「1mってどれくらい?」と聞くと、すぐにイメージできなかったり…。こちらが「単位も書こうね」と声をかけると、「なんで?」と不思議そうな顔をすることもあります。
でもこれは、子どもたちの理解が足りないというよりも、「学んだこと」と「日常の感覚」がつながっていないだけなんだと思います。
マックスでは、理科や社会もふくめて、生活と教科書の内容を自然につなげる工夫をしています。おうちでも「これって何cmぐらいかな?」「1gってどのくらいだろう?」といった会話が、きっと子どもたちの“気づき”につながります。
□ よくあるNGな教え方とその理由
×「とにかく割れば出るでしょ?」→ なぜ割るのかの理由が伝わらず、定着しません。
×「この式 覚えちゃえばいいよ」→ 計算式だけ覚えると、他の問題で応用ができなくなります。
✅ その代わりに:「対応表にしてみよう」や「1あたりを出すとわかりやすいよ」などの声かけを!
□ 最後に
単位量の理解は、算数や理科の基礎です。 対応表を使うことで、解答への道すじが「見える化」され、子ども自身の理解が深まります。
また、この “1あたりの数”の考え方は、速さ・割合・平均などの中学・高校内容にもつながります。今のうちに感覚をつかんでおくことで、将来の算数・数学・理科もラクになります!
合格屋マックスでは、このような「考え方を経験する」指導を大切にしています。
お子さんの「できた!」を育てるサポート、ぜひご家庭でも参考にしてみてください。
合格屋マックスの算数教室でした。
😊「なんだ。簡単じゃん」と感じてもらえたらすごくうれしいです。わかりにくい問題があったら、教えてください。簡単に説明したり、わかりやすい他の方法で、もっと楽に理解が深まります。
「ブログより実際に話しがしたい」「もっといろいろ教えてほしい!」と感じた人は、無料体験や相談に来てください! この先生に相談をすることや習うことができます! 少し勇気を出して、ぜひ一度体験しに来てください! 「わかるって面白い」とか成績が良くなる自分を感じられる日がきます。お問い合わせ・ご質問はこちらです。








